
【题目】如图,⊙O是锐角△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.下列结论:①AF平分∠BAC;②点F为△BDC的外心;③![]() ;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是_____(把你认为正确结论的序号都填上).
;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是_____(把你认为正确结论的序号都填上).
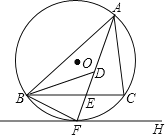
【答案】①②③④
【解析】
如图1,连接OF,CF,通过切线的性质证OF⊥FH,进而由FH∥BC,得OF⊥BC,即可由垂径定理得到F是弧BC的中点,根据圆周角定理可得∠BAF=∠CAF,可得AF平分∠BAC;由三角形外角性质和同弧所对的圆周角相等可得∠BDF=∠FBD,可得BF=DF=CF,可得点F为△BDC的外心;如图2,过点C作CG∥AB,交AF的延长线于点G,通过证明△BAE∽△CGE,可得![]() ,即可判断③;如图3,作点M关于AF的对称点M',当点N在线段BM'上,且BM'⊥AC时,BN+MN有最小值为BM',即可判断④.
,即可判断③;如图3,作点M关于AF的对称点M',当点N在线段BM'上,且BM'⊥AC时,BN+MN有最小值为BM',即可判断④.
解:如图1,连接OF,CF,
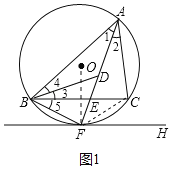
∵FH是⊙O的切线,
∴OF⊥FH,
∵FH∥BC,
∴OF⊥BC,且OF为半径,
∴OF垂直平分BC,
∴![]() =
=![]() ,
,
∴∠1=∠2,BF=CF,
∴AF平分∠BAC,故①正确,
∵∠1=∠2,∠4=∠3,∠5=∠2,
∴∠1+∠4=∠2+∠3,
∴∠1+∠4=∠5+∠3,
∵∠1+∠4=∠BDF,∠5+∠3=∠FBD,
∴∠BDF=∠FBD,
∴BF=FD,且BF=CF,
∴BF=DF=CF,
∴点F为△BDC的外心,故②正确;
如图2,过点C作CG∥AB,交AF的延长线于点G,
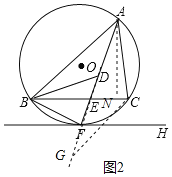
∵CG∥AB,
∴∠BAE=∠EGC,且∠BAE=∠CAE,
∴∠CAE=∠CGE,
∴AC=CG,
∵CG∥AB,
∴△BAE∽△CGE,
∴![]() ,
,
∴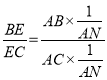 =
=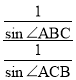 =
=![]() ,
,
故③正确;
如图3,作点M关于AF的对称点M',
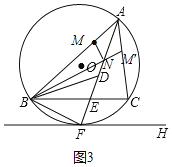
∵点M与点M'关于AF对称,
∴MN=M'N,
∴BN+MN=BN+M'N,
∴当点N在线段BM'上,且BM'⊥AC时,BN+MN有最小值为BM',且sin∠BAC=![]() ,
,
∴BN+MN最小值为ABsin∠BAC,
故④正确,
故答案为:①②③④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】把分别标有数字1,2,3,4的四个小球放入A袋内,把分别标有数字-1,-2,-2,-3,5的五个小球放入B袋内,所有的小球除了标有的数字不同外,其余完全相同.
(1)学生甲从A、B两个袋子中各摸出一个小球,求这两个小球上的数字互为相反数的概率.
(2)当B袋中标有5的小球的数字变为 时,(1)中的概率为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
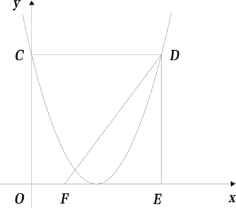
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于点C,过点C作CD∥
轴交于点C,过点C作CD∥![]() 轴交该函数的图象于点D,过点D作DE∥
轴交该函数的图象于点D,过点D作DE∥![]() 轴交
轴交![]() 轴于点E,已知点F(1,0),连接DF.
轴于点E,已知点F(1,0),连接DF.
(1)请求出该函数图象的项点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)如图,若该二次函数的图象的顶点落在![]() 轴上,P为对称轴右侧抛物线上一点;
轴上,P为对称轴右侧抛物线上一点;
①连接PD、PE、PF,若![]() ,求点P的坐标;
,求点P的坐标;
②若∠PFD=![]() ∠DEF,点P的横坐标为m,则m的值为 .
∠DEF,点P的横坐标为m,则m的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
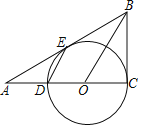
【题目】如图,点D、O在△ABC的边AC上,以CD为直径的⊙O与边AB相切于点E,连结DE、OB,且DE∥OB.
(1)求证:BC是⊙O的切线.
(2)设OB与⊙O交于点F,连结EF,若AD=OD,DE=4,求弦EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
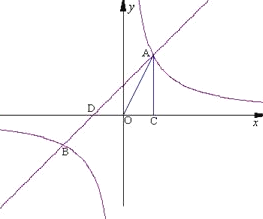
【题目】如图,已知反比例函数![]() (k1>0)与一次函数
(k1>0)与一次函数![]() 相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.

(1)如图1,取点M(1,0),则点M到直线l:y=![]() x﹣1的距离为多少?
x﹣1的距离为多少?
(2)如图2,点P是反比例函数y=![]() 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=
在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
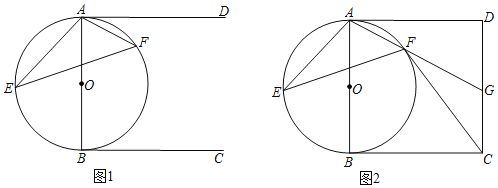
【题目】已知,AB是⊙O的直径,E、F是⊙O上的点,连接AE、AF、EF,BC是⊙O的切线,过点A作AD∥BC.
(1)如图1,求证:∠DAF=∠AEF;
(2)如图2,若AD=BC=AB,连接CD,延长AF交CD于G,连接CF,若FC=BC=4,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
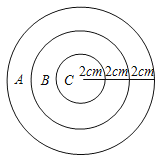
【题目】如图为一个封闭的圆形装置,整个装置内部为A、B、C三个区域(A、B两区域为圆环,C区域为小圆),具体数据如图.
(1)求出A、B、C三个区域三个区域的面积:SA= ,SB= ,SC= ;
(2)随机往装置内扔一粒豆子,多次重复试验,豆子落在B区域的概率PB为多少?
(3)随机往装置内扔180粒豆子,请问大约有多少粒豆子落在A区域?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有![]() 个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共
个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共![]() 组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做
组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做![]() 次试验,汇总起来后,摸到红球次数为
次试验,汇总起来后,摸到红球次数为![]() 次.
次.
![]() 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?
![]() 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com