
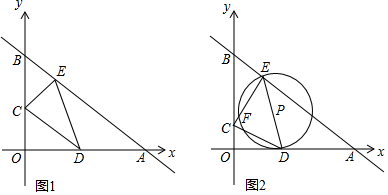
���� ��1���������A��B�������꣬�������������λ����Ǻ������EC���ɣ�
��2���������������ۼ��ɢ���ͼ2�У�����D���A�غ�ʱ����DCE��ֱ�������Σ�����ͼ3�У�����CDE=90��ʱ����CDE��ֱ�������Σ�
��3����ͼ4�У�����DF����DH��AB��H�����ı���EFDH�Ǿ��Σ�����֤��EH=AH������AB=10���г����̼��ɽ�����⣮
��� �⣺��1����ͼ1�У�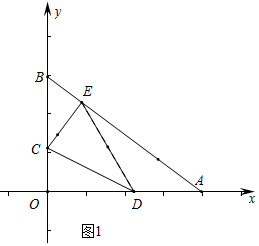
����ֱ��ֱ��y=-$\frac{3}{4}$x+6����x=0�õ�y=6����y=0�õ�x=8��
��A��8��0����B��0��6��
��OA=8��OB=6��
��AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��BC=t��sin��ABO=$\frac{OA}{AB}$=$\frac{EC}{BC}$��
��$\frac{8}{10}$=$\frac{EC}{t}$��
��EC=$\frac{4}{5}$t��
�ʴ�Ϊ10��$\frac{4}{5}$t��
��2������ͼ2�У�����D���A�غ�ʱ����DCE��ֱ�������Σ�
��OC=6-t��OD=2OC=12-2t��
��12-2t=8��
��t=2s
����ͼ3�У�����CDE=90��ʱ����CDE��ֱ�������Σ�
��EH��OA��H��
��E��$\frac{12}{25}$t��6-$\frac{9}{25}$t����
�ɡ�COD�ס�DHE�õ���$\frac{DH}{EH}$=$\frac{CO}{OD}$=$\frac{1}{2}$��
��EH=2DH��
��6-$\frac{9}{25}$t=2[$\frac{12}{25}$t-��12-2t��]��
���t=$\frac{750}{133}$s��
����������t��ֵΪ2s��$\frac{750}{133}$sʱ����DCE��ֱ�������Σ�
��3����ͼ4�У�����DF����DH��AB��H�����ı���EFDH�Ǿ��Σ�
��EF=$\frac{3}{5}$DE��
��sin��EDF=$\frac{3}{5}$=sin��BAO��
���EDF=��DAH��
��DF��EH��
���DEH=��EDF=��EAD��
��DE=DA����DH��AE��
��EH=AH��
��BE=$\frac{3}{5}$t��OD=12-2t��
��AD=8-��12-2t��=2t-4��
��EH=AH=$\frac{4}{5}$•��2t-4����
��AB=10��
��$\frac{3}{5}$t+$\frac{8}{5}$��2t-4��=10��
��t=$\frac{82}{19}$s��
��t=$\frac{82}{19}$sʱ��EF=$\frac{3}{5}$DE��
�ʴ�Ϊ$\frac{82}{19}$s��
���� ���⿼��Բ�ۺ��⡢һ�κ�����Ӧ�á����������ε��ж������ʡ����ε��ж������ʡ����������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | -$\frac{1}{2}$ | C�� | -2 | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-4��3�� | B�� | ��3��-4�� | C�� | ��2��-6�� | D�� | ��-6��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
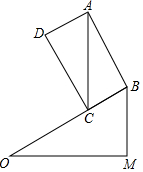 ��ͼ�����¶ȱ�Ϊ1��$\sqrt{3}$�������ϣ�����һ��������ľ�飬��֪AC=5��AC��OM��OB=10����ľ����б����ÿ��2����λ���ٶ����»���������C���O�غ�ʱֹͣ����ľ�黬����ʱ��Ϊ���룮
��ͼ�����¶ȱ�Ϊ1��$\sqrt{3}$�������ϣ�����һ��������ľ�飬��֪AC=5��AC��OM��OB=10����ľ����б����ÿ��2����λ���ٶ����»���������C���O�غ�ʱֹͣ����ľ�黬����ʱ��Ϊ���룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+a3=a5 | B�� | a3��a2=a | C�� | a2•a3=a6 | D�� | ��a2��3=a5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3.14 | B�� | -�� | C�� | 0 | D�� | $\sqrt{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
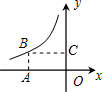 ��ͼ������OABC�ϣ���A��C�ֱ���x��y���ϣ���B�ڷ�����y=$\frac{k}{x}$λ�ڵڶ�����ͼ���ϣ��������Ϊ6����k��ֵ�ǣ�������
��ͼ������OABC�ϣ���A��C�ֱ���x��y���ϣ���B�ڷ�����y=$\frac{k}{x}$λ�ڵڶ�����ͼ���ϣ��������Ϊ6����k��ֵ�ǣ�������| A�� | 3 | B�� | 6 | C�� | -6 | D�� | -3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com