
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.

【答案】(1)![]() ,直角三角形;(2)
,直角三角形;(2)![]() ;(3)M1(
;(3)M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() ).
).
【解析】
试题分析:(1)先确定出点A,B坐标,再用待定系数法求出抛物线解析式;用勾股定理逆定理判断出△ABC是直角三角形;
(2)根据运动表示出OP=2t,CQ=10﹣t,判断出Rt△AOP≌Rt△ACQ,得到OP=CQ即可;
(3)分三种情况用平面坐标系内,两点间的距离公式计算即可.
试题解析:(1)∵直线y=﹣2x+10与x轴,y轴相交于A,B两点,∴A(5,0),B(0,10),∵抛物线过原点,∴设抛物线解析式为![]() ,∵抛物线过点B(0,10),C(8,4),∴
,∵抛物线过点B(0,10),C(8,4),∴![]() ,∴
,∴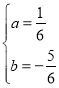 ,∴抛物线解析式为
,∴抛物线解析式为![]() ,∵A(5,0),B(0,10),C(8,4),∴
,∵A(5,0),B(0,10),C(8,4),∴![]() =
=![]() =125,
=125,![]() =
=![]() =100,
=100,![]() =
=![]() =25,∴
=25,∴![]() ,∴△ABC是直角三角形.
,∴△ABC是直角三角形.
(2)如图1,当P,Q运动t秒,即OP=2t,CQ=10﹣t时,由(1)得,AC=OA,∠ACQ=∠AOP=90°,在Rt△AOP和Rt△ACQ中,∵AC=OA,PA=QA,∴Rt△AOP≌Rt△ACQ,∴OP=CQ,∴2t=10﹣t,∴t=![]() ,∴当运动时间为
,∴当运动时间为![]() 时,PA=QA;
时,PA=QA;

(3)存在,∵![]() ,∴抛物线的对称轴为x=
,∴抛物线的对称轴为x=![]() ,∵A(5,0),B(0,10),∴AB=
,∵A(5,0),B(0,10),∴AB=![]()
设点M(![]() ,m);
,m);
①若BM=BA时,∴![]() ,∴m1=
,∴m1=![]() ,m2=
,m2=![]() ,∴M1(
,∴M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() );
);
②若AM=AB时,∴![]() ,∴m3=
,∴m3=![]() ,m4=
,m4=![]() ,∴M3(
,∴M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() );
);
③若MA=MB时,∴![]() ,∴m=5,∴M(
,∴m=5,∴M(![]() ,5),此时点M恰好是线段AB的中点,构不成三角形,舍去;
,5),此时点M恰好是线段AB的中点,构不成三角形,舍去;
∴点M的坐标为:M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() ).
).


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】国家规定,中、小学生每天在校体育活动时间不低于1h,为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h. 
根据上述信息解答下列问题:
(1)本次调查数据的中位数落在组内;
(2)若该辖区约有20000名学生,请估计其中达到国家规定体育活动时间的人数;
(3)若A组取t=0.25h,B组取t=0.75h,C组取t=1.25h,D组取t=2h,试计算这300名学生平均每天在校体育活动的时间(结果精确到0.1h).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于点Q,PQ=4,PE=1. 
(1)求∠BPQ的度数;
(2)求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)在y轴上找出一点P,使得PA+PB的值最小,直接写出点P的坐标;
(3)在平面直角坐标系中,找出一点A2 , 使△A2BC与△ABC关于直线BC对称,直接写出点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2007年某校初中三个年级在校学生共796名,学生的出生月份统计如下,根据图中数据回答以下问题:
(1)出生人数少于60人的月份有哪些?
(2)至少有两个人生日在10月5日是不可能事件,还是可能事件,还是必然事件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】君畅中学计划购买一些文具送给学生,为此学校决定围绕“在笔袋、圆规、直尺、钢笔四种文具中,你最需要的文具是什么?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据以上信息回答下列问题:
(1)在这次调查中,最需要圆规的学生有多少名?并补全条形统计图;
(2)如果全校有970名学生,请你估计全校学生中最需要钢笔的学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com