
����Ŀ�������У�����ϲ���Ѵ��͵ı����۳���![]() ����״���۵����̰�ͼ�������������ܵ�˳����У�������Ӱ���ֱ�ʾֽ���ķ��棩���������ֽ�۳ɵij�����ֽ����ͼ�٣���Ϊ
����״���۵����̰�ͼ�������������ܵ�˳����У�������Ӱ���ֱ�ʾֽ���ķ��棩���������ֽ�۳ɵij�����ֽ����ͼ�٣���Ϊ![]() ���ף��ֱ�ش��������⣺
���ף��ֱ�ش��������⣺

![]() ���������ֽ���Ŀ�Ϊ
���������ֽ���Ŀ�Ϊ![]() ���ף����ҿ�ʼ�۵�ʱ���
���ף����ҿ�ʼ�۵�ʱ���![]() ���
���![]() �ľ���Ϊ
�ľ���Ϊ![]() ���ף���ô��ͼ���У�
���ף���ô��ͼ���У�![]() ________���ף���ͼ���У�
________���ף���ͼ���У�![]() ________���ף�
________���ף�
![]() ���������ֽ���Ŀ�Ϊ
���������ֽ���Ŀ�Ϊ![]() ���ף��ֲ���Ҫ�۳�ͼ�ܵ���״������Ϊ�����ۣ�ϣ��ֽ�����˳�����
���ף��ֲ���Ҫ�۳�ͼ�ܵ���״������Ϊ�����ۣ�ϣ��ֽ�����˳�����![]() �ij�����ȣ�������ͼ������Գ�ͼ�Σ������ڿ�ʼ�۵�ʱ���
�ij�����ȣ�������ͼ������Գ�ͼ�Σ������ڿ�ʼ�۵�ʱ���![]() ���
���![]() �ľ��루�����
�ľ��루�����![]() ��ʾ����
��ʾ����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2��2ax+b��x�ύ��A��B��3��0�����㣬��y�ύ�ڵ�C����OC=3OA���������ߵĶ���ΪD��
��1���������ߵĽ���ʽ��
��2���������߶Գ�����Ҳ�����������Ƿ���ڵ�P��ʹ����PDC�ǵ��������Σ������ڣ�������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3����ƽ����x���ֱ����������߽���M��N���㣨���е�M�ڵ�N���Ҳࣩ����x�����Ƿ���ڵ�Q��ʹ��MNQΪ����ֱ�������Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ű�����ͬ�Ŀ�ƬA��B��C��D����Ƭ������ֱ�ӡ���������Ρ�ƽ���ı��Ρ�Բ��������Σ���Щ��Ƭ��ͼ����ͬ�⣬�������ͬ�����������ſ�Ƭ��������ϴ�Ⱥ������в�����
��1���������ȡ����һ�ſ�Ƭ���鵽�Ŀ�Ƭ�������ĶԳ�ͼ��������Գ�ͼ�εĸ������� ����
��2����������һ�Ų��Żأ�Ȼ���ٴ����µij��һ�ţ�������״ͼ���б���ʾ���������ſ�Ƭ���п��ܵĽ�������������ſ�Ƭ��ͼ�������ĶԳ�ͼ�εĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �����������
�����������![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ��
��![]() �ڲ�ͬ��
�ڲ�ͬ��![]() ����һ�㣻
����һ�㣻![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ��ʱ����ת���ã���ת�Ƕ�Ϊ
��ʱ����ת���ã���ת�Ƕ�Ϊ![]() �������н��ۣ�
�������н��ۣ�
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��һ��ֱ���ϣ�
��һ��ֱ���ϣ�
��![]() ��
��
��![]() ��
��
������ȷ���У� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1�����ı���ABCD�У�AB=BC=CD=DA=5 cm��BD=8 cm����AC= cm��
��2���ڿ�Ϊ8 cm �ij�����ֽ���ϣ���ͼ1�е��ı��������ͼ2��ʾ��ͼ����
�������7��ͼ1�е��ı������ͼ������ô������Ҫ cm����ֽ����
����ͼ1�е��ı�����x���������ֽ����Ϊy cm����y��x֮��ĺ�������ʽ��
���ڳ�Ϊ40 cm��ֽ���ϣ��������ַ������������ƶ��ٸ�ͼ1�е��ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����Ϊ1����һ�β������ֱ��ӳ�AB��BC��CA����A1��B1��C1��ʹA1B��AB��B1C��BC��C1A��CA��˳������A1��B1��C1���õ���A1B1C1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1����A2��B2��C2��ʹA2B1��A1B1��B2C1��B1C1��C2A1��C1A1��˳������A2��B2��C2���õ���A2B2C2�������˹��ɣ�Ҫʹ�õ��������ε��������2013�����پ���_____�β�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() �Ḻ���ύ�ڵ�
�Ḻ���ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ��
��![]() ����
����![]() ����Ҳࣩ����
����Ҳࣩ����![]() ���������϶Գ����ϵ�һ���㣬��
���������϶Գ����ϵ�һ���㣬��![]() �����Ϊ
�����Ϊ![]() ��
��
��1����![]() ��ֵ��
��ֵ��
��2��![]() �����Ϊ
�����Ϊ![]() ��ֱ��д��
��ֱ��д��![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������������ǰ��ˮ���ӵĺ������ͼ��ʾ�����б�ˮ������������dz�Ϊ![]() �ס���Ϊ
�ס���Ϊ![]() �ľ��Σ����轫�����������������������£��ٽ���ˮ��
�ľ��Σ����轫�����������������������£��ٽ���ˮ��![]() ���¶���
���¶���![]() ��Ϊ
��Ϊ![]() ������һ���뱳ˮ���泤�ߴ�ֱ��ƽ���߽���ˮ����ֳ�
������һ���뱳ˮ���泤�ߴ�ֱ��ƽ���߽���ˮ����ֳ�![]() ����ͬ�ľ����������������ֲ����Ի���
����ͬ�ľ����������������ֲ����Ի���

��1��������ˮ����������
��2������Ի��ijɱ���ÿƽ����![]() Ԫ���ֲݵijɱ���ÿƽ����
Ԫ���ֲݵijɱ���ÿƽ����![]() Ԫ����ô��ֲ����������Ҫ����Ԫ��
Ԫ����ô��ֲ����������Ҫ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
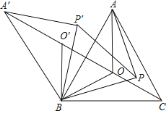
����Ŀ������ABC�У�AB=AC����D��ֱ��BC��һ�㣨����B��C�غϣ�����ADΪһ����AD���Ҳ�����ADE��ʹAD=AE����DAE =��BAC������CE��
��1����ͼ1������D���߶�BC�ϣ������BAC=90��������BCE=________�ȣ�
��2����![]() ��
��![]() ��
��
����ͼ2���������߶�BC���ƶ�����![]() ��
��![]() ֮����������������ϵ����˵�����ɣ�
֮����������������ϵ����˵�����ɣ�
�ڵ�����ֱ��BC���ƶ�����![]() ��
��![]() ֮����������������ϵ����ֱ��д����Ľ��ۣ�
֮����������������ϵ����ֱ��д����Ľ��ۣ�




�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com