
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O. 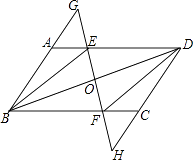
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAE=∠DCF,
在△ABE和△CDF中, 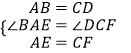 ,
,
∴△ABE≌△CDF(SAS)
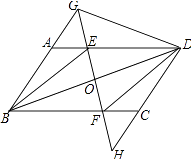
(2)解:四边形BEDF是菱形;理由如下:如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OB=OD,
∵DG=BG,
∴EF⊥BD,
∴四边形BEDF是菱形.
【解析】(1)由平行四边形的性质得出AB=CD,∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;(2)由平行四边形的性质得出AD∥BC,AD=BC,证出DE=BF,得出四边形BEDF是平行四边形,得出OB=OD,再由等腰三角形的三线合一性质得出EF⊥BD,即可得出四边形BEDF是菱形.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD. 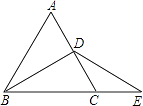
(1)用尺规作图的方法,过点D作DM⊥BE,垂足为M(不写作法,只保留作图痕迹);
(2)若AB=2,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P(a,b)在函数y= ![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y= ![]() 的一个“派生函数”.例如:点(2,
的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y= ![]() 的图象上,则函数y=2x2+
的图象上,则函数y=2x2+ ![]() 称为函数y=
称为函数y= ![]() 的一个“派生函数”.现给出以下两个命题: ①存在函数y=
的一个“派生函数”.现给出以下两个命题: ①存在函数y= ![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧
的一个“派生函数”,其图象的对称轴在y轴的右侧
②函数y= ![]() 的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
的所有“派生函数”,的图象都经过同一点,下列判断正确的是( )
A.命题①与命题②都是真命题
B.命题①与命题②都是假命题
C.命题①是假命题,命题②是真命题
D.命题①是真命题,命题②是假命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y= ![]() x﹣3与反比例函数y=
x﹣3与反比例函数y= ![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 , k的值为;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y= ![]() 的图象,当y≥﹣2时,请直接写出自变量x的取值范围.
的图象,当y≥﹣2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=( ) 
A.105°
B.110°
C.130°
D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于钝角α,定义它的三角函数数值如下: sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α).
(1)求sin135°,cos150°的值;
(2)若一个三角形的三个内角的比为1:1:4,A,B是这个三角形的两个顶点,且∠A≤∠B,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m值及∠A,∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在150≤x<175之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
组别 | 身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据图表提供的信息,有下列几种说法
①估计报名者中男生身高的众数在D组;
②估计报名者中女生身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④估计身高在160cm至170cm(不含170cm)的学生约有400人
其中合理的说法是( )
A.①②
B.①④
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)试求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com