练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】解方程：

    （1）9x2﹣36＝0

    （2）x2﹣6x+5＝0

    （3）x2﹣4x+8＝0

    （4）（x﹣4）2﹣（5﹣2x）2＝0

    【答案】（1）x1＝﹣2，x2＝2；（2）x1＝1，x2＝5；（3）x1＝x2＝2；（4）x1＝1，x2＝3．

    【解析】

    （1）方程利用因式分解法求出解即可；

    （2）方程利用因式分解法求出解即可；

    （3）方程利用因式分解法求出解即可；

    （4）方程利用因式分解法求出解即可．

    （1）方程分解因式得：9（x+2）（x﹣2）＝0，

    可得x+2＝0或x﹣2＝0，

    解得：x1＝﹣2，x2＝2；

    （2）分解因式得：（x﹣1）（x﹣5）＝0，

    可得x﹣1＝0或x﹣5＝0，

    解得：x1＝1，x2＝5；

    （3）分解因式得：（x﹣2）2＝0，

    解得：x1＝x2＝2；

    （4）分解因式得：（x﹣4+5﹣2x）（x﹣4﹣5+2x）＝0，

    解得：x1＝1，x2＝3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知：梯形ABCD中，∠ABC＝90°，∠DAB＝45°，AB∥DC，DC＝3，AB＝5，点P在AB边上，以点A为圆心AP为半径作弧交边DC于点E，射线EP于射线CB交于点F．

    （1）若AP，求DE的长；

    （2）联结CP，若CP＝EP，求AP的长；

    （3）线段CF上是否存在点G，使得△ADE与△FGE相似？若相似，求FG的值；若不相似，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 黄石知名特产“黄石港饼”“白鸭牌松花皮蛋”“珍珠果米酒”一直以来享有美誉，深受人们喜爱．端午节快到了，为了满足市场需求，某公司组织20辆汽车装运港饼、皮蛋、米酒共120吨去外地销售，按计划20辆汽车都要装满，且每辆汽车只能装运同一类食品，根据下表提供的信息解答以下问题．

    港饼

    皮蛋

    米酒

    每辆汽车载重量（吨）

    8

    6

    5

    每吨食品获利（万元）

    0.2

    0.4

    0.6

    （1）设装运港饼的车辆为x辆，装运皮蛋的车辆为y辆，求y与x之间的函数关系式；

    （2）此次销售获利为W万元，试求W关于x的函数关系式；

    （3）如果装运每种食品的车辆都不少于2辆，那么怎样安排车辆能使此次销售获利最大？并求出最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某文具店第一次用1600元购进了一批新型文具试销，很快卖完，于是第二次又用5000元购进了这款文具，但第二次的进价是第一次进价的1.25倍，购进数量比第一次多300件.

    （1）求该文具店第一次购进这款文具的进价；

    （2）已知该文具店将第一次购进的这款文具按50%的利润率定价销售完后，第二次购进的这款文具售价在原来售价的基础上增加5a%，销售了第二次购进的这款文具的12a%，剩下的这款文具9折处理，销售一空，结果该文具店前后两次销售这款文具共获利3000元，求a的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线经过B、C两点，顶点D在正方形内部．

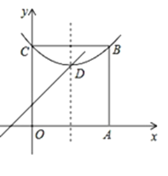
    （1）直接写出点D（m，n）所有的特征线 ;

    （2）若点D有一条特征线是y=x+1，求此抛物线的解析式；

    （3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于y轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

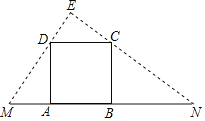
    【题目】如图，在边长为6的正方形ABCD的一边AB在线段MN上移动，连接MD，NC并延长交于点E，MN＝18．

    （1）当AM＝4时，求CN长；

    （2）若∠E＝90°，求证AM＝BN；

    （3）△MNE能否为等腰三角形？若能，求出AM的长，若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC=13，BC=10，点D为BC的中点，DE⊥AB于点E，则tan∠BDE的值等于（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程．

    已知：如图，⊙O及⊙O上一点P．

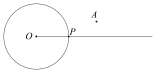
    求作：过点P的⊙O的切线．

    作法：如图，作射线OP；

    ① 在直线OP外任取一点A，以A为圆心，AP为半径作⊙A，与射线OP交于另一点B；

    ②连接并延长BA与⊙A交于点C；

    ③作直线PC；

    则直线PC即为所求．根据小元设计的尺规作图过程，

    （1）使用直尺和圆规，补全图形；（保留作图痕迹）

    （2）完成下面的证明：

    证明：∵ BC是⊙A的直径，

    ∴ ∠BPC=90° （填推理依据）．

    ∴ OP⊥PC．

    又∵ OP是⊙O的半径，

    ∴ PC是⊙O的切线 （填推理依据）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学活动：

    问题情境：有这样一个问题：探究函数的图象与性质，小明根据学习函数的经验，对函数的图象与性质进行了探究．

    问题解决：下面是小明的探究过程，请补充完整：

    （1）函数的自变量的取值范围是 ；

    （2）表是与的几组对应值．

    …

    -4

    -3

    -2

    -1

    1

    2

    3

    4

    …

    …

    0

    -1

    3

    2

    …

    求的值；

    （3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象．

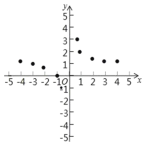
    （4）结合函数的图象，写出该函数的性质（两条即可）

    查看答案和解析>>

    同步练习册答案