
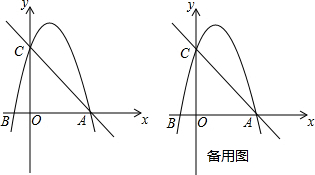
分析 (1)结合图形,根据点A的坐标和已知条件OA=OC=4OB得到点B、C的坐标;然后利用待定系数法求该抛物线的解析式即可;
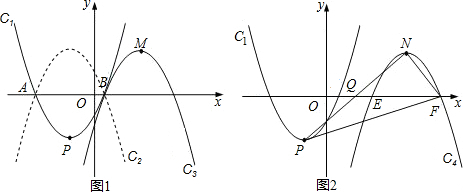
(2)如图2,过点C作CP⊥AC.交抛物线于点P,过点P作PM⊥y轴于点M,构建等腰直角△MCP,则MC=MP.设P(m,-m2+3m+4),结合图形得到:OM=OC+MC=OC+PM=4+m,即4+m=-m2+3m+4,通过解方程求得m的值,则易求点P的纵坐标;
(3)连接OD,由题意知,矩形OFDE的对角线相等:OD=EF,据垂线段最短,可知:当OD⊥AC时,OD最短,即EF最短.由勾股定理和三角形中位线定理易推知:$DF=\frac{1}{2}OC=2$,所以点P的纵坐标是2.最后根据二次函数图象上点的坐标特征来求点P的横坐标即可.
解答 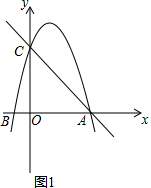 解:(1)如图1,∵A(4,0),
解:(1)如图1,∵A(4,0),
∴OA=4.
又∵OA=OC=4OB,
∴OC=4,OB=1,
∴B(-1,0),C(0,4).
设抛物线的解析式为:
y=a(x+1)(x-4)
把C(0,4)代入得:4=a×1×(-4),
∴a=-1,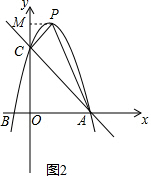
∴y=-(x+1)(x-4)y=-x2+3x+4,
∴抛物线的解析式为:y=-x2+3x+4;
(2)存在.理由如下:
如图2,过点C作CP⊥AC.交抛物线于点P,过点P作PM⊥y轴于点M.
∵OA=OC,
∴∠OCA=45°.
又∵∠PC⊥AC,
∴∠PCA=90°,
∴∠MCP=∠MPC=45°,
∴MC=MP.
∵P在抛物线上.
∴设P(m,-m2+3m+4),
∴OM=OC+MC=OC+PM=4+m,
∴4+m=-m2+3m+4,
∴m2-2m=0,
∴m1=0(舍去),m2=2,
∴-m2+3m+4=6,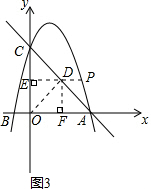
∴P(2,6);
(3)连接OD,由题意知,四边形OFDE是矩形,则OD=EF,据垂线段最短,可知:
当OD⊥AC时,OD最短,即EF最短.
由(1)知,在Rt△AOC中,OC=OA=4,
∴$AC=4\sqrt{2}$.
又∵D为AC的中点.
∴DF∥OC,
∴$DF=\frac{1}{2}OC=2$,
∴点P的纵坐标是2.
∴-x2+3x+4=2,
∴$x=\frac{{3±\sqrt{17}}}{2}$,
∴当EF最短时,点$P(\frac{{3+\sqrt{17}}}{2},2)$或$(\frac{{3-\sqrt{17}}}{2},2)$.
点评 本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求抛物线的解析式,勾股定理以及等腰三角形的判定与性质.在求有关动点问题时,利用几何法解题要注意分析题意,分情况讨论结果.在本解答中,是利用代数法解答(3)题的.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
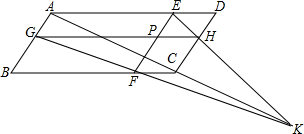 如图,设P为?ABCD内任意一点,过P作EF∥AB,GH∥BC,EF交A,BC于点E,F,GH交AB,DC于点G,H,且AC,GF,EH不平行.求证:AC,GF,EH相交于一点.
如图,设P为?ABCD内任意一点,过P作EF∥AB,GH∥BC,EF交A,BC于点E,F,GH交AB,DC于点G,H,且AC,GF,EH不平行.求证:AC,GF,EH相交于一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com