
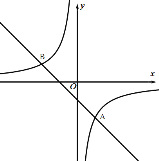
【题目】如图,一次函数的图象![]() 与反比例函数的图象
与反比例函数的图象![]() 交于A(2,﹣4),B(m, 2)两点.当x满足条件______________时,一次函数的值大于反比例函数值.
交于A(2,﹣4),B(m, 2)两点.当x满足条件______________时,一次函数的值大于反比例函数值.
科目:初中数学 来源: 题型:
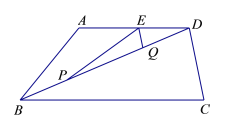
【题目】如图,在梯形ABCD中,AD∥BC,BC=BD=10,CD=4,AD=6.点P是线段BD上的动点,点E、Q分别是线段DA、BD上的点,且DE=DQ=BP,联结EP、EQ.
(1)求证:EQ∥DC;
(2)如果△EPQ是以EQ为腰的等腰三角形,求线段BP的长;
(3)当BP=m(0<m<5)时,求∠PEQ的正切值.(用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段AB上有一点C,在AB的同侧作等腰△ACD和等腰△ECB,且AC=AD,EC=EB,∠DAC=∠CEB,直线BD与线段AE,线段CE分别交于点F,G.对于下列结论:①△DCG∽△BEG;②△ACE∽△DCB;③GF·GB=GC·GE;④若∠DAC=∠CEB=90°,则2AD2=DF·DG.其中正确的是( )
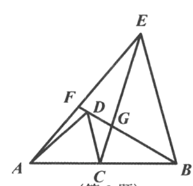
A.①②③④B.①②③C.①③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作AB的垂线交AC的延长线于点F.
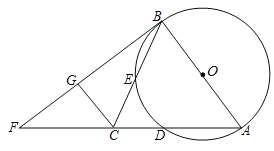
(1)求证:![]() ;
;
(2)过点C作CG⊥BF于G,若AB=5,BC=2![]() ,求CG,FG的长.
,求CG,FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=![]() 的图象上,当-3≤x≤-1时,求函数值y的取值范围.
的图象上,当-3≤x≤-1时,求函数值y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
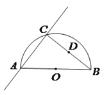
【题目】如图,AB是半圆O的直径,AB=10,过点A的直线交半圆于点C,且sin∠CAB=![]() ,连结BC,点D为BC的中点.已知点E在射线AC上,△CDE与△ACB相似,则线段AE的长为________;
,连结BC,点D为BC的中点.已知点E在射线AC上,△CDE与△ACB相似,则线段AE的长为________;
查看答案和解析>>
科目:初中数学 来源: 题型:
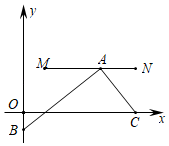
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.![]() ≤b≤1B.
≤b≤1B.![]() ≤b≤1C.
≤b≤1C.![]() ≤b≤
≤b≤![]() D.
D.![]() ≤b≤1
≤b≤1
查看答案和解析>>
科目:初中数学 来源: 题型:
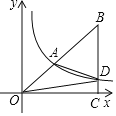
【题目】如图,反比例函数y=![]() (x>0)的图象经过Rt△BOC斜边上的中点A,与边BC交于点D,连接AD,则△ADB的面积为( )
(x>0)的图象经过Rt△BOC斜边上的中点A,与边BC交于点D,连接AD,则△ADB的面积为( )
A.12B.16C.20D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,对于任意两点![]() ,
,![]() ,若点
,若点![]() 满足
满足![]() ,
,![]() ,那么称点
,那么称点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
例如:![]() ,
,![]() ,当点
,当点![]() 满是
满是![]() ,
,![]() 时,则点
时,则点![]() 是点
是点![]() ,
,![]() 的融合点,
的融合点,

(1)已知点![]() ,
,![]() ,
,![]() ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.
(2)如图,点![]() ,点
,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
①试确定![]() 与
与![]() 的关系式.
的关系式.
②若直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com