
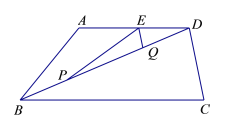
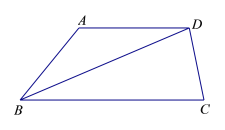
【题目】如图,在梯形ABCD中,AD∥BC,BC=BD=10,CD=4,AD=6.点P是线段BD上的动点,点E、Q分别是线段DA、BD上的点,且DE=DQ=BP,联结EP、EQ.
(1)求证:EQ∥DC;
(2)如果△EPQ是以EQ为腰的等腰三角形,求线段BP的长;
(3)当BP=m(0<m<5)时,求∠PEQ的正切值.(用含m的式子表示)
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用两边成比例且夹角相等可判定△DEQ ∽△BCD,从而证得结论;
(2)设BP的长为x,则DQ=x,QP=2x-10,利用(1)的结论△DEQ ∽△BCD,求得![]() .分类讨论:当EQ=EP、QE=QP时,分别求得答案即可;
.分类讨论:当EQ=EP、QE=QP时,分别求得答案即可;
(3)过点P作PH⊥EQ,交EQ的延长线于点H;过点B作BG⊥DC,垂足为点G,易证得△PHQ ∽△BGD,利用对应边成比例通过计算得到![]() 的值,从而求得答案.
的值,从而求得答案.
(1)∵AD//BC,∴∠EDQ=∠DBC.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴△DEQ ∽△BCD.
∴∠DQE=∠BDC,
∴EQ//CD.
(2)设BP的长为x,则DQ=x,QP=2x-10.
∵△DEQ ∽△BCD,
∴![]() ,
,
∴![]() .
.
(i)当EQ=EP时,
∴∠EQP =∠EPQ,
∵DE=DQ,∴∠EQP =∠QED,∴∠EPQ =∠QED,
∴△EQP ∽△DEQ,∴![]() ,∴
,∴![]() ,
,
解得 ![]() ,或
,或![]() (舍去).
(舍去).
(ii)当QE=QP时,
∴![]() ,解得
,解得 ![]() ,
,
∵![]() ,∴此种情况不存在.
,∴此种情况不存在.
∴![]()
(3)过点P作PH⊥EQ,交EQ的延长线于点H;过点B作BG⊥DC,垂足为点G.

∵BD=BC,BG⊥DC,∴DG=2,BG![]() ,
,
∵BP= DQ=m,∴PQ=10-2m.
∵EQ∥DC∴∠PQH =∠BDG.
又∵∠PHQ =∠BGD= 90°,
∴△PHQ ∽△BGD.
∴![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,
,
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了预防“流感”,某学校在休息日用“药熏”消毒法对教室进行消毒.已知药物释放过程中,室内每立方米的含药量y(毫克)与时间x(时)成正比例;药物释放结束后,y与x成反比例;如图所示,根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数解析式;
(2)据测定,当药物释放结束后,每立方米的含药量降至0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多长时间,学生才能进入教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,N为边AD上一点,连接BN.过点A作AP⊥BN于点P,连接CP,M为边AB上一点,连接PM,∠PMA=∠PCB,连接CM,有以下结论:①△PAM∽△PBC;②PM⊥PC;③M、P、C、B四点共圆;④AN=AM.其中正确的个数为( )
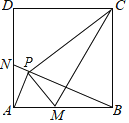
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A>∠B,分别以点A,C为圆心,大于![]() AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于
AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于![]() BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
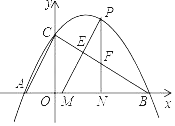
【题目】如图,二次函数y=ax2+bx+![]() 的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
(1)求这个二次函数的解析式;
(2)求线段PE最大值,并求出线段PE最大时点P的坐标;
(3)若S△PMN=3S△PEF时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
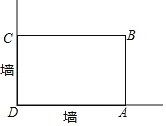
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(Ⅰ)若花园的面积是252m2,求AB的长;
(Ⅱ)当AB的长是多少时,花园面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15m时,飞行时间是多少?
(2)在飞行过程中,小球从飞出到落地所用时间是多少?
(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2-4ax+4(a≠0)与y轴交于点A.过点B(0,3)作y轴的垂线l,若抛物线y=ax2-4ax+4(a≠0)与直线l有两个交点,设其中靠近y轴的交点的横坐标为m,且│m│<1,则a的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
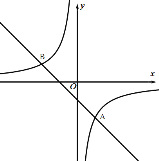
【题目】如图,一次函数的图象![]() 与反比例函数的图象
与反比例函数的图象![]() 交于A(2,﹣4),B(m, 2)两点.当x满足条件______________时,一次函数的值大于反比例函数值.
交于A(2,﹣4),B(m, 2)两点.当x满足条件______________时,一次函数的值大于反比例函数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com