
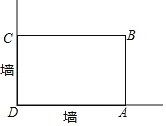
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(Ⅰ)若花园的面积是252m2,求AB的长;
(Ⅱ)当AB的长是多少时,花园面积最大?最大面积是多少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校决定从甲、乙两名同学中选拔一人参加“诵读经典”大赛,在相同的测试条件下,甲、乙两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83.
乙:88,81,85,81,80.
请回答下列问题:
(1)甲成绩的中位数是______,乙成绩的众数是______;
(2)经计算知![]() ,
,![]() .请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
.请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.
(1)求证:△CBE为等边三角形;
(2)若AD=5,DE=7,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
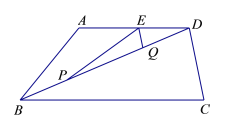
【题目】如图,在梯形ABCD中,AD∥BC,BC=BD=10,CD=4,AD=6.点P是线段BD上的动点,点E、Q分别是线段DA、BD上的点,且DE=DQ=BP,联结EP、EQ.
(1)求证:EQ∥DC;
(2)如果△EPQ是以EQ为腰的等腰三角形,求线段BP的长;
(3)当BP=m(0<m<5)时,求∠PEQ的正切值.(用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形,且相似比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )
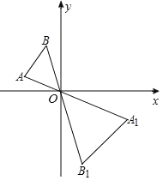
A.(2,-4)B.(1,-4)C.(-1,4)D.(-4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取一点O,以点O为圆心,OF为半径作⊙O与AD相切于点P.AB=6,BC=![]()
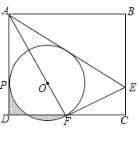
(1)求证:F是DC的中点.
(2)求证:AE=4CE.
(3)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
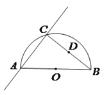
【题目】如图,AB是半圆O的直径,AB=10,过点A的直线交半圆于点C,且sin∠CAB=![]() ,连结BC,点D为BC的中点.已知点E在射线AC上,△CDE与△ACB相似,则线段AE的长为________;
,连结BC,点D为BC的中点.已知点E在射线AC上,△CDE与△ACB相似,则线段AE的长为________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com