
【题目】如图1,以AB为直径作⊙O,点C是直径AB上方半圆上的一点,连结AC,BC,过点C作∠ACB的平分线交⊙O于点D,过点D作AB的平行线交CB的延长线于点E.
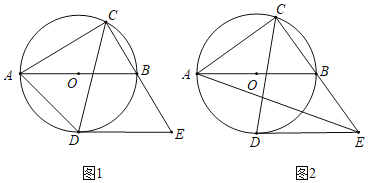
(1)如图1,连结AD,求证:∠ADC=∠DEC.
(2)若⊙O的半径为5,求CACE的最大值.
(3)如图2,连结AE,设tan∠ABC=x,tan∠AEC=y,
①求y关于x的函数解析式;
②若![]() =
=![]() ,求y的值.
,求y的值.
【答案】(1)详见解析;(2)100;(3)①y=![]() ;②y=
;②y=![]() 或
或![]() .
.
【解析】
(1)根据AB∥DE,可得∠ABC=∠E,又由同圆中同弧所对圆周角相等可得∠ADC=∠E;
(2)先找出△ADC∽△DEC,即可得到CD2=CACE,再根据圆的半径为5可知最大为CD=5,即CACE=100;
(3)①由(2)的相似可得y=tan∠AEC=![]() ,再过点D作DF⊥CE,设EF=a,∴CF=DF=ax,CD=
,再过点D作DF⊥CE,设EF=a,∴CF=DF=ax,CD=![]() ax,代入y即可得到y=
ax,代入y即可得到y=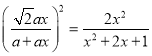 .
.
②根据![]() =
=![]() ,得到
,得到![]() =9:4,即x:y=9:4,代入y的表达式即可求出结果.
=9:4,即x:y=9:4,代入y的表达式即可求出结果.
(1)证明:∵AB∥DE,
∴∠ABC=∠E,
∵∠ADC=∠ABC,
∴∠ADC=∠E;
(2)解:∵CD平分∠ACB,
∴∠ACD=∠DCE,
又∠ADC=∠E,
∴△ADC∽△DEC,
∴![]() ,
,
即CD2=CACE,
又∵⊙O的半径为5,
∴CACE=CD2≤102=100.
即CACE的最大值为100.
(3)解:①连接AD,

∵△ADC∽△DEC,![]() ,
,
∴y=tan∠AEC=![]() ,
,
过点D作DF⊥CE,不妨设EF=a,
∵∠CED=∠CBA,∠DCE=45°,
∴CF=DF=ax,
∴CD=![]() ax,
ax,
∴y=![]() =
=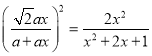 ..
..
②∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =9:4,
=9:4,
即x:y=9:4,
将y=![]() x代入y=
x代入y=![]() 得,
得,
![]() =
=![]() ,
,
解得,x1=2,x2=![]() ,
,
当x=2时,y=![]() ,
,
当x=![]() 时,y=
时,y=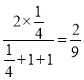 ,,
,,
∴y=![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在数轴上,点![]() 表示1,现将点
表示1,现将点![]() 沿
沿![]() 轴做如下移动,第一次点
轴做如下移动,第一次点![]() 向左移动3个单位长度到达
向左移动3个单位长度到达![]() ,第二次将点
,第二次将点![]() 向右移动6个单位长度到达点
向右移动6个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动9个单位长度到达点
向左移动9个单位长度到达点![]() ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第![]() 次移动到点
次移动到点![]() ,那么
,那么![]() 表示的数是____.
表示的数是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2-mx-m-1的图像交x轴于A、B两点(A、B分别位于坐标原点O的左、右两侧),交y轴于点C,且△ABC的面积为6.
(1)求这个二次函数的表达式;
(2)若P为平面内一点,且PB=3PA,试求当△PAB的面积取得最大值时点P的坐标,并求此时直线PO将△ABC分成的两部分的面积之比.
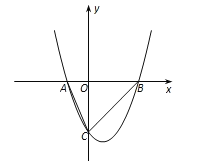
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,其中记载:“今有甲、乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八。问甲、乙二人原持钱各几何?”译文:“甲,乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文,如果乙得到甲所有钱的![]() ,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】缙云山是国家级自然风景名胜区,上周周末,小明和妈妈到缙云山游玩,登上了香炉峰观景塔,从观景塔底中心![]() 处水平向前走
处水平向前走![]() 米到
米到![]() 点处,再沿着坡度为
点处,再沿着坡度为![]() 的斜坡
的斜坡![]() 走一段距离到达
走一段距离到达![]() 点,此时回望观景塔,更显气势宏伟,在
点,此时回望观景塔,更显气势宏伟,在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 再往前沿水平方向走
再往前沿水平方向走![]() 米到
米到![]() 处,观察到观景塔顶端的仰角是
处,观察到观景塔顶端的仰角是![]() ,则观景塔的高度
,则观景塔的高度![]() 为( )(tan22°≈0.4)
为( )(tan22°≈0.4)
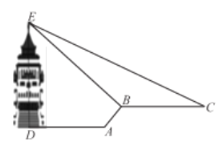
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
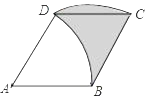
A. 2cm2B. 4![]() cm2C. 4cm2D. πcm2
cm2C. 4cm2D. πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形,线段的垂直一部分线是线段的对称轴,如图直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() 是
是![]() 上任一点,连结
上任一点,连结![]() 、
、![]() ,将线段
,将线段![]() 与直线
与直线![]() 对称,我们发现
对称,我们发现![]() 与
与![]() 完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
已知:如图,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() 上的任意一点.
上的任意一点.
求证:![]() .
.
图中的两个直角三角形![]() 和
和![]() ,只要证明这两个三角形全等,便可证明
,只要证明这两个三角形全等,便可证明![]() (请写出完整的证明过程)
(请写出完整的证明过程)
请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程,定理应用.
(1)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 的垂直平分线.
的垂直平分线.
求证:直线![]() 、
、![]() 、
、![]() 交于点.
交于点.
(2)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_______.
的长为_______.
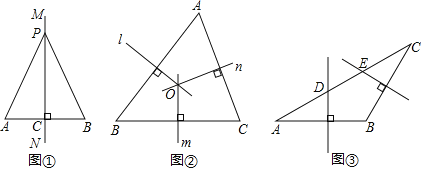
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com