练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．计算：（$\sqrt{10}$-2）（$\sqrt{10}$+2）=6．

    分析 直接利用平方差公式计算得出即可．

    解答 解：（$\sqrt{10}$-2）（$\sqrt{10}$+2）
    =（$\sqrt{10}$）2-4
    =10-4
    =6．
    故答案为：6．

    点评 此题主要考查了二次根式的混合运算，正确应用平方差公式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

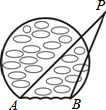    14．如图，两灯塔A、B间的距离恰好为暗礁所在的圆的半径，要使船P不驶入暗礁区，则航行中应保持∠P（　　）
    A．大于60°B．大于30°C．小于60°D．小于30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图所示，已知△ABC中，∠BAC=45°，AD⊥BC于D，BD=2，CD=3，试求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

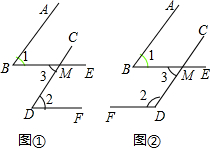    7．已知一个角的两边与另一个角的两边分别平行，请结合图，探索这两个角之间的关系，并说明理由．
    （1）如图①，AB∥CD，BE∥DF，∠1与∠2的关系是相等；
    证明：
    （2）如图②，AB∥CD，BE∥DF，∠1与∠2的关系是互补；
    证明：
    （3）经过上述证明，我们可得出结论，如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补；
    （4）若这两个角的两边分别平行，且一个角比另一个角的3倍少60°，则这两个角分别是多少度？
    解：

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．计算：（x-1）2-（x+2）（x-2）=-2x+5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，F在DE的延长线上，且AF=CE．
    （1）求证：AE=BE；
    （2）求证：四边形ACEF是平行四边形；
    （3）当∠B满足什么条件时，四边形ACEF是菱形？证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）$|{-\frac{1}{2}}|-\sqrt{9}+{（π-4）^0}-sin{30°}$
    （2）-14-（-2）0+2tan45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．设m、n是一元二次方程x2+2x-5=0的两个根，则m2+3m+n=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

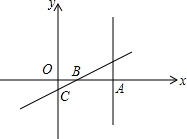    6．已知，直线x=2与x轴相交于点A，动直线y=0.5x+b分别与x轴，y轴相交于点B、C，点D在直线x=2上．
    （1）若AD=1.5，∠DBC=45°，求b的值．
    （2）若△DBC与△OBC相似，求点D的坐标．

    查看答案和解析>>

    同步练习册答案