
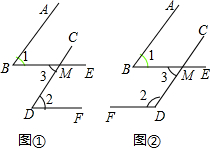
 ��֪һ���ǵ���������һ���ǵ����߷ֱ�ƽ�У�����ͼ��̽����������֮��Ĺ�ϵ����˵�����ɣ�
��֪һ���ǵ���������һ���ǵ����߷ֱ�ƽ�У�����ͼ��̽����������֮��Ĺ�ϵ����˵�����ɣ����� ��1������ƽ���ߵ������á�1=��3����2=��3�����1=��2��
��2������ƽ���ߵ������á�1=��3����2+��3=180�㣬���ԡ�1+��2=180�㣻
��3���ɣ�1���ͣ�2���Ľ��۽��лش�
��4����һ���ǵĶ���Ϊx������һ���ǵĶ���Ϊ3x-60�㣬���ݣ�3���Ľ��۽������ۣ�x=3x-60���x+3x-60��=180�㣬Ȼ��ֱ�ⷽ�����x����ɵõ���Ӧ�����ǵĶ�����
��� �⣺��1����1=��2��
֤�����£���AB��CD��
���1=��3��
��BE��DF��
���2=��3��
���1=��2��
��2����1+��2=180�㣮
֤�����£���AB��CD��
���1=��3��
��BE��DF��
���2+��3=180�㣬
���1+��2=180�㣻
��3�����һ���ǵ���������һ���ǵ����߷ֱ�ƽ�У���ô����������Ȼ���
��4����һ���ǵĶ���Ϊx������һ���ǵĶ���Ϊ3x-60�㣬
��x=3x-60�㣬���x=30�㣬���������ǵĶ����ֱ�Ϊ30�㣬30�㣻
��x+3x-60��=180�㣬���x=60�㣬���������ǵĶ����ֱ�Ϊ60�㣬120�㣮
�ʴ�Ϊ����ȣ���������Ȼ���
���� ���⿼����ƽ�������ʣ���ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У�ͬ���ڽǻ�������ֱ��ƽ�У��ڴ�����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
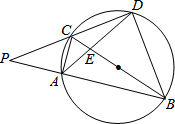 ��ͼ��ʾ��BCΪԲ��ֱ����ͼ�����������εĶ������У�������
��ͼ��ʾ��BCΪԲ��ֱ����ͼ�����������εĶ������У�������| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 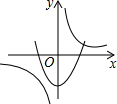 | C�� | 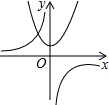 | D�� | 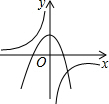 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
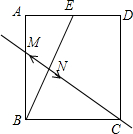 ��ͼ������ֽƬABCD�У���E��AD���е㣬��AE=1������BE���ֱ���B��EΪԲ�ģ��Դ���$\frac{1}{2}BE$�ij�Ϊ�뾶�������������ڵ�M��N����ֱ��MNǡ�ù���C����AB�ij���Ϊ��������
��ͼ������ֽƬABCD�У���E��AD���е㣬��AE=1������BE���ֱ���B��EΪԲ�ģ��Դ���$\frac{1}{2}BE$�ij�Ϊ�뾶�������������ڵ�M��N����ֱ��MNǡ�ù���C����AB�ij���Ϊ��������| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | $\sqrt{5}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
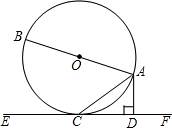 ��ͼ��AB�ǡ�O��ֱ����AC���ң�ֱ��EF������C��AD��EF�ڵ�D����DAC=��BAC��
��ͼ��AB�ǡ�O��ֱ����AC���ң�ֱ��EF������C��AD��EF�ڵ�D����DAC=��BAC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��㶫ʡ÷�������꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ������
����x��1����x+3��=x2+px��3����p=_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com