
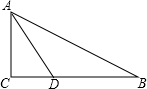
 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,BD=5,求AC的长.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,BD=5,求AC的长.  夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:选择题
| A. | 掷一枚普通正六面体骰子,所得点数不超过6 | |
| B. | 买一张彩票中奖 | |
| C. | 太阳从西边落下 | |
| D. | 口袋中装有10个红球,从中摸出一个是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,8) | B. | (-6,-2) | C. | (0,-2) | D. | (-6,8) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
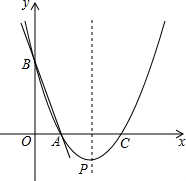 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
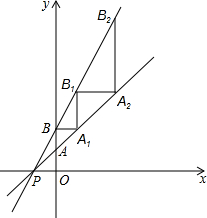 如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )| A. | (63,64) | B. | (65,64) | C. | (31,32) | D. | (127,128) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com