
分析 (1)设甲图书的单价为x元/本,则乙图书的单价为(x-4)元/本,根据:3000元购进甲种图书的数量=2400元购进乙种图书的数量相同列出方程求解即可;
(2)购买甲种图书m,则购买乙图书(100-m)本,根据:所需经费=甲图书总费用+乙图书总费用可列函数关系式;
(3)根据:总经费W≤1820且购买的甲种图书的数量≥乙种图书数量列出不等式组,解不等式组即可的不等式组的解集,从而确定方案.
解答 解:(1)设甲图书的单价为x元/本,则乙图书的单价为(x-4)元/本,根据题意,
得:$\frac{3000}{x}=\frac{2400}{x-4}$,
解得:x=20,
经检验x=20是原方程的根,
则x-4=16,
答:甲图书的单价为20元/本,则乙图书的单价为16元/本.
(2)购买甲种图书m,则购买乙图书(100-m)本,根据题意,
有:W=20m+16(100-m)=4m+1600;
(3)根据题意,得:$\left\{\begin{array}{l}{4m+1600≤1820}\\{m≥100-m}\end{array}\right.$,
解得:50≤m≤55,
∵m需取整数,
∴m的值可以是:50,51,52,53,54,55,
故购买方案有6种:①甲图书50本,乙图书50本;②甲图书51本,乙图书49本;③甲图书52本,乙图书48本;④甲图书53本,乙图书47本;⑤甲图书54本,乙图书46本;⑥甲图书55本,乙图书45本.
点评 本题主要考查分式方程、一次函数、不等式组的综合应用能力,根据题意准确抓住相等关系或不等关系是解题的根本和关键.


科目:初中数学 来源: 题型:解答题
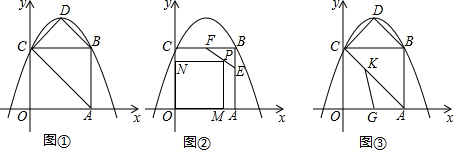
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
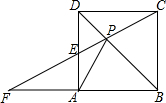 如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.
如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
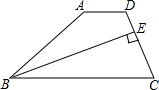 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )| A. | $\frac{7}{4}$ | B. | $\frac{5}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
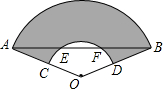 如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.
如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com