
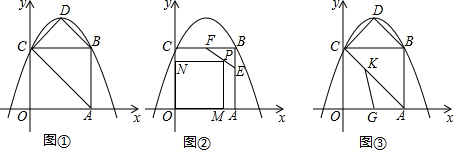
分析 (1)由正方形OABC的边长为4可得出点C、点B的坐标,代入抛物线解析式中得到关于b、c的二元一次方程,解方程即可得出b、c的值,从而得出抛物线的解析式,将抛物线解析式配方即可得到顶点D的坐标,将四边形ABDC分成两个三角形,由三角形的面积公式即可得出四边形ABDC的面积;
(2)根据截法找出直线EF的解析式,设出P点坐标(x,y),由矩形面积=长×宽可得出S关于x的函数关系式,由函数关系式在x的取值范围内的单调性即可解决最值问题;
(3)过K作KT⊥CB于点T,可找出KC=$\sqrt{2}$KT,由时间=路程÷速度找出时间t=GK+KT,由GK+KT≥4即可得出结论.
解答 解:(1)由已知得:C(0,4),B(4,4),
把B与C坐标代入y=-$\frac{1}{2}$x2+bx+c得:$\left\{\begin{array}{l}{4=c}\\{4=-8+4b+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=4}\end{array}\right.$,
故此抛物线的解析式为y=-$\frac{1}{2}$x2+2x+4.
∵y=-$\frac{1}{2}$x2+2x+4=-$\frac{1}{2}$(x-2)2+6,
∴抛物线顶点坐标为(2,6).
S四边形ABDC=S△ABC+S△BCD=$\frac{1}{2}$×4×4+$\frac{1}{2}$×4×2=8+4=12.
(2)∵在正方形上截去一角,成为五边形,
∴存在线段EF且EF的位置已经固定,且E(4,3),F(2,4),
∴直线EF的解析式为y=-$\frac{1}{2}$x+5.
设P(x,y)(2≤x≤4),则PM=y=-$\frac{1}{2}$x+5,PN=x,
∴S=PM•PN=xy=-$\frac{1}{2}{x}^{2}$+5x(2≤x≤4),
∵S=-$\frac{1}{2}{x}^{2}$+5x=-$\frac{1}{2}(x-5)^{2}$+$\frac{25}{2}$,
∴当2≤x≤4时,S随x的增大而增大,
∴当x=4时,矩形PMON面积最大为12,此时点P坐标为(4,3).
(3)过K作KT⊥CB于点T,如图所示.
∵∠ACB=45°,
∴KC=$\sqrt{2}$KT.
运动时间t=$\frac{GK}{1}+\frac{KC}{\sqrt{2}}$=$\frac{GK}{1}+\frac{\sqrt{2}KT}{\sqrt{2}}$=GK+KT≥4,
∴当KG⊥OA时,最短时间为4秒,此时点K的坐标为(2,2).
点评 本题考查了待定系数法求函数解析式、二次函数的性质、三角形的面积公式以及正方形的性质,解题的关键:(1)由待定系数法求函数解析式;(2)寻找在x的取值范围内面积S的最值;(3)找出时间t=GK+KT.本题属于中档题,难度不大,(1)没有难度;(2)巧妙的利用P点的横纵坐标表示矩形的面积;(3)通过作图,利用数形结合化复杂为简洁.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 掷一枚普通正六面体骰子,所得点数不超过6 | |
| B. | 买一张彩票中奖 | |
| C. | 太阳从西边落下 | |
| D. | 口袋中装有10个红球,从中摸出一个是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{a+4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
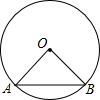 如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )
如图,AB是⊙O的弦,已知∠OAB=30°,AB=4,则⊙O的半径为( )| A. | 4 | B. | 2 | C. | $2\sqrt{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
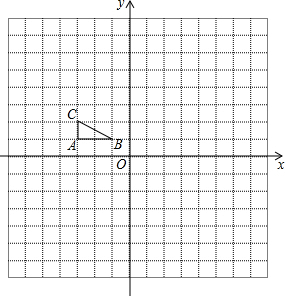 如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
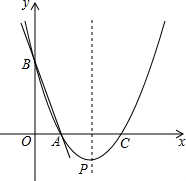 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com