
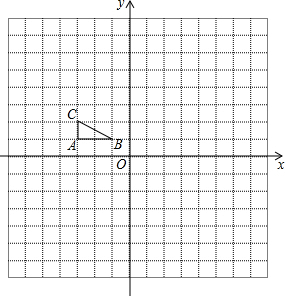
 如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.分析 (1)利用网格特点和旋转的性质画出点A、B、C的对应点A1、B1、C1,从而得到△A1B1C1;
(2)利用关于原点中心对称的点的特征特征,把A、B、C点的横纵坐标都乘以-2得到A2、B2、C2的坐标,然后描点即可得到△A2B2C2.
解答 解:(1)如图,△A1B1C1为所作,点C1的坐标为(2,3);
(2)如图,△A2B2C2为所作.
故答案为(2,3).
点评 本题考查了位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了旋转变换.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数 | 4 | 6 | 8 | 2 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 95和85 | B. | 90和85 | C. | 90和87.5 | D. | 85和87.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
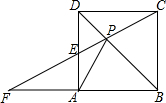 如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.
如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
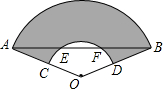 如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.
如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
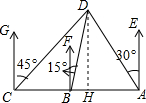 如图,在一笔直的海岸线上有A,B,C3个观测站,B,C都在A的正西方向,AC=100($\sqrt{3}+1$)km,从C测得船D在北偏东45°的方向,从B测得船D在北偏东15°的方向,从A测得船D在北偏西30°的方向.
如图,在一笔直的海岸线上有A,B,C3个观测站,B,C都在A的正西方向,AC=100($\sqrt{3}+1$)km,从C测得船D在北偏东45°的方向,从B测得船D在北偏东15°的方向,从A测得船D在北偏西30°的方向.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com