
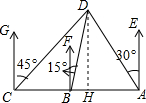
 如图,在一笔直的海岸线上有A,B,C3个观测站,B,C都在A的正西方向,AC=100($\sqrt{3}+1$)km,从C测得船D在北偏东45°的方向,从B测得船D在北偏东15°的方向,从A测得船D在北偏西30°的方向.
如图,在一笔直的海岸线上有A,B,C3个观测站,B,C都在A的正西方向,AC=100($\sqrt{3}+1$)km,从C测得船D在北偏东45°的方向,从B测得船D在北偏东15°的方向,从A测得船D在北偏西30°的方向.分析 (1)设AD为xkm,根据正、余弦的定义用x表示出AH、DH,根据题意列出方程,解方程即可;
(2)作BG⊥AD于G,设AB为ykm,根据三角函数的定义用y表示出AG、DG,解方程即可.
解答 解:(1)设AD为xkm,
由题意得,∠DAH=60°,
则∠ADH=30°,
∴AH=$\frac{1}{2}$AD=$\frac{1}{2}$x,DH=$\frac{\sqrt{3}}{2}$x,
∵∠DCH=45°,
∴CH=DH=$\frac{\sqrt{3}}{2}$x,
∴$\frac{1}{2}$x+$\frac{\sqrt{3}}{2}$x=100($\sqrt{3}+1$),
解得,x=200,即AD=200km;
(2)作BG⊥AD于G,
设AB为ykm,
则AG=$\frac{1}{2}$ykm,BG=$\frac{\sqrt{3}}{2}$ykm,
∵∠DBA=75°,∠DAB=60°,
∴∠BDA=45°,
∴DG=BG=$\frac{\sqrt{3}}{2}$ykm,
∴$\frac{1}{2}$y+$\frac{\sqrt{3}}{2}$y=200,
解得,y=200($\sqrt{3}$-1)≈146.0km,
答:观测点A与观测点B的距离AB约为146.0km.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的定义是解题的关键.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
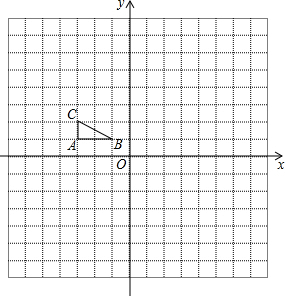 如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,8) | B. | (-6,-2) | C. | (0,-2) | D. | (-6,8) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
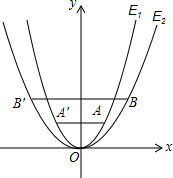 如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
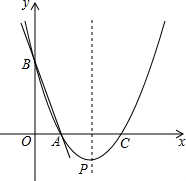 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com