
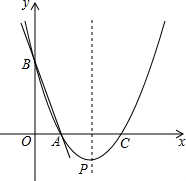
 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.分析 (1)根据之变量与函数值得对应关系,可得A、B点坐标,根据待定系数法,可得答案;
(2)根据梯形的中位线,可得DG的长,根据DG与AB的关系,可得答案,根据勾股定理,可得关于m的方程,根据解方程,可得答案;
(3)根据正方形的对角线互相垂直,相等且平分,可得M、N的坐标,根据勾股定理,可得AN的长.
解答 (1)解:∵直线y=-3x+3与x轴、y轴分别交于点A、B,
∴A(1,0),B(0,3).
又∵抛物线抛物线y=a(x-2)2+k经过点A(1,0),B(0,3),
∴$\left\{\begin{array}{l}{a+k=0}\\{4a+k=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{k=-1}\end{array}\right.$,
故a,k的值分别为1,-1;
(2)证明:如图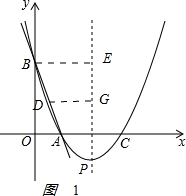 ,
,
取AB中点D,作DG⊥对称轴于G,对称轴x=2交x轴于点F,过点B作BE垂直于直线x=2于点E.
则DG=$\frac{1}{2}$(BE+AF)=$\frac{3}{2}$<$\frac{\sqrt{10}}{2}$=$\frac{1}{2}$AB
∴抛物线的对称轴与以AB为直径的圆一定相交.
设Q点的坐标为(2,m),
∵AB为直径,∴∠AQB=90°,
∴AQ2+BQ2=AB2.
在Rt△AQF中,AQ2=AF2+QF2=1+m2,
在Rt△BQE中,BQ2=BE2+EQ2=4+(3-m)2,
∴1+m2+4+(3-m)2=10,
∴m1=1,m2=2,
∴Q点的坐标为(2,2)或(2,1);
(3)如图2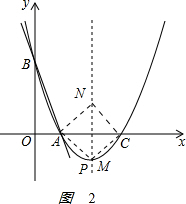 ,
,
当点N在对称轴上时,NC与AC不垂直,所以AC应为正方形的对角线.
又∵对称轴x=2是AC的中垂线,
∴M点与顶点P(2,-1)重合,N点为点P关于x轴的对称点,其坐标为(2,1).
此时,MF=NF=AF=CF=1,且AC⊥MN,
∴四边形AMCN为正方形.
在Rt△AFN中,AN=$\sqrt{A{F}^{2}+N{F}^{2}}$=$\sqrt{2}$,即正方形的边长为$\sqrt{2}$.
点评 本题考查了二次函数综合题,利用待定系数求函数解析式;利用梯形的中位线得出DG的长是解题关键;利用正方形的性质得出M、N的坐标是解题关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
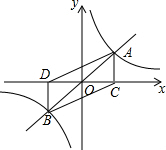 如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.
如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
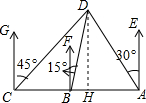 如图,在一笔直的海岸线上有A,B,C3个观测站,B,C都在A的正西方向,AC=100($\sqrt{3}+1$)km,从C测得船D在北偏东45°的方向,从B测得船D在北偏东15°的方向,从A测得船D在北偏西30°的方向.
如图,在一笔直的海岸线上有A,B,C3个观测站,B,C都在A的正西方向,AC=100($\sqrt{3}+1$)km,从C测得船D在北偏东45°的方向,从B测得船D在北偏东15°的方向,从A测得船D在北偏西30°的方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com