
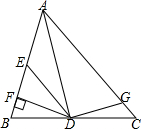
 AD为∠BAC平分线,DF⊥AB,DE=DG,S△ADG=50,S△ADE=39,求S△EDF.
AD为∠BAC平分线,DF⊥AB,DE=DG,S△ADG=50,S△ADE=39,求S△EDF. 分析 作DM=DE交AC于M,作DN⊥AC,利用角平分线的性质得到DN=DF,将三角形EDF的面积转化为三角形DNM的面积来求.
解答 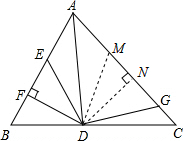 解:作DM=DE交AC于M,作DN⊥AC于点N,
解:作DM=DE交AC于M,作DN⊥AC于点N,
∵DE=DG,
∴DM=DG,
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DN,
在Rt△DEF和Rt△DMN中,
$\left\{\begin{array}{l}{DN=DF}\\{DM=DE}\end{array}\right.$,
∴Rt△DEF≌Rt△DMN(HL),
∵△ADG和△AED的面积分别为50和39,
∴S△MDG=S△ADG-S△ADM=50-39=11,
S△DNM=S△EDF=$\frac{1}{2}$S△MDG=$\frac{1}{2}$×11=5.5.
点评 本题考查了角平分线的性质及全等三角形的判定及性质,解题的关键是正确地作出辅助线,将所求的三角形的面积转化为另外的三角形的面积来求.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | $\frac{1}{10}$ | C. | 1 | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
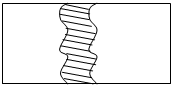 如图,在一块长为12cm,宽为6cm的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2cm),则空白部分表示的草地面积是60cm2.
如图,在一块长为12cm,宽为6cm的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2cm),则空白部分表示的草地面积是60cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
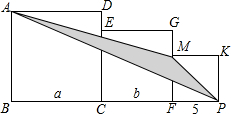 如图,已知三个正方形的边长分别为a厘米、b厘米、5厘米.
如图,已知三个正方形的边长分别为a厘米、b厘米、5厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com