
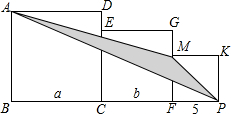
 如图,已知三个正方形的边长分别为a厘米、b厘米、5厘米.
如图,已知三个正方形的边长分别为a厘米、b厘米、5厘米.分析 (1)由AC∥PM,得S△APM=S△CPM,由此即可解决问题.
(2)代入(1)中结论即可.
解答 解:(1)如图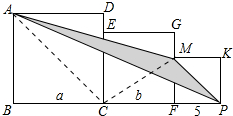 连接AC、CM.
连接AC、CM.
∵四边形ABCD,MFPK是正方形,
∴∠ACB=∠MPF=45°,
∴AC∥MP,
∴S△APM=S△CPM=$\frac{1}{2}$•CP•MF=$\frac{1}{2}$(b+5)•5=$\frac{25}{2}$+$\frac{5b}{2}$.
(2)当b=4$\sqrt{3}$时,S△APM=$\frac{25}{2}$+10$\sqrt{3}$.
点评 本题考查正方形的性质、整式的混合运算等知识,解题的关键是把△APM的面积转化为△CPM的面积,记住同底等高的三角形面积相等,属于中考常考题型.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com