
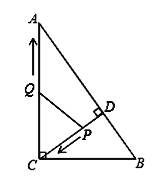
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=8ЃЌBC=6ЃЌCDЁЭABгкЕуDЃЎЕуPДгЕуD ГіЗЂЃЌбиЯпЖЮDCЯђЕуCдЫЖЏЃЌЕуQДгЕуCГіЗЂЃЌбиЯпЖЮCAЯђЕуAдЫЖЏЃЌСНЕуЭЌЪБГіЗЂЃЌЫйЖШЖМЮЊУПУы1ИіЕЅЮЛГЄЖШЃЌЕБЕуPдЫЖЏЕНCЪБЃЌСНЕуЖМЭЃжЙЃЎЩшдЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉЧѓЯпЖЮCDЕФГЄЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЁїCPQЪЧжБНЧШ§НЧаЮЃП
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЕУPQЗжЁїACDЕФУцЛ§ЮЊ1ЃК11ЃПШєДцдкЃЌЧѓГіtЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉCD=![]() ЃЛЃЈ2ЃЉtЮЊ3УыЛђ
ЃЛЃЈ2ЃЉtЮЊ3УыЛђ![]() УыЃЛЃЈ3ЃЉЕБ
УыЃЛЃЈ3ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЪБЪЙЕУPQЗжЁїACDЕФУцЛ§ЮЊ1ЃК11ЃЎ
ЪБЪЙЕУPQЗжЁїACDЕФУцЛ§ЮЊ1ЃК11ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШРћгУЙДЙЩЖЈРэЧѓГіABЃН10ЃЌНјРћгУУцЛ§ЗЈЧѓГіCDЃЛ
ЃЈ2ЃЉЯШБэЪОГіCPЃЌдйХаЖЯГіЁЯACDЃНЁЯBЃЌНјЖјЗжСНжжЧщПіЃЌРћгУЯрЫЦШ§НЧаЮЕУГіБШР§ЪННЈСЂЗНГЬЧѓНтЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШХаЖЯГіЁїCEQЁзЁїCDAЃЌЕУГі![]() ЃЌНјЖјБэЪОГіQEЃН
ЃЌНјЖјБэЪОГіQEЃН![]() tЃЌдйЗжЕБSЁїCPQЃН
tЃЌдйЗжЕБSЁїCPQЃН![]() SЁїACDЪБЃЌКЭЕБSЁїCPDЃН
SЁїACDЪБЃЌКЭЕБSЁїCPDЃН![]() SЁїACDЪБЃЌРћгУУцЛ§НЈСЂЗНГЬЧѓНтМДПЩЕУГіНсТлЃЎ
SЁїACDЪБЃЌРћгУУцЛ§НЈСЂЗНГЬЧѓНтМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉдкRtЁїABCжаЃЌИљОнЙДЙЩЖЈРэЕУЃЌABЃН![]()
ЁпSЁїABCЃН![]() ACBCЃН
ACBCЃН![]() ABCDЃЌ
ABCDЃЌ
ЁрCDЃН![]() ЃЌ
ЃЌ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЃЌCDЃН![]() ЃЌ
ЃЌ
гЩдЫЖЏжЊЃЌCQЃНtЃЌDPЃНtЃЌ
ЁрCPЃНCDDPЃН![]() tЃЌ
tЃЌ
ЁпЁЯACBЃН90ЁуЃЌ
ЁрЁЯACDЃЋЁЯBCDЃН90ЁуЃЌ
ЁпCDЁЭABЃЌ
ЁрЁЯBЃЋЁЯBCDЃН90ЁуЃЌ
ЁрЁЯACDЃНЁЯBЃЌ
ЁпЁїCPQгыЁїABCЯрЫЦЃЌ
ЂйЕБЁЯCPQЃН90ЁуЪБЃЌЁїCPQЁзЁїBCAЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр
ЁрtЃН3
ЂкЕБЁЯCQPЃН90ЁуЪБЃЌЁїCPQЁзЁїBACЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр
ЁрtЃН![]() ЃЌ
ЃЌ
МДЃКtЮЊ3УыЛђ![]() УыЪБЃЌЁїCPQгыЁїABCЯрЫЦЃЎ
УыЪБЃЌЁїCPQгыЁїABCЯрЫЦЃЎ
ЃЈ3ЃЉМйЩшДцдкЃЌШчЭМЃЌ
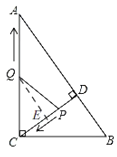
RtЁїACDжаЃЌИљОнЙДЙЩЖЈРэЕУЃЌADЃН![]() ЃЌ
ЃЌ
Й§ЕуQзїCEЁЭCDгкEЃЌ
ЁрQEЁЮADЃЌ
ЁрЁїCEQЁзЁїCDAЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр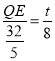
ЁрQEЃН![]()
ЁпSЁїCPQЃН![]() CPQEЃН
CPQEЃН![]() ЃЈ
ЃЈ![]() ЃЉ
ЃЉ![]()
ЁрSЁїACDЃН![]() ADCDЃН
ADCDЃН![]() ЁС
ЁС![]() ЁС
ЁС![]() ЃЌ
ЃЌ
ЁпPQЗжЁїACDЕФУцЛ§ЮЊ1ЃК11ЃЌ
ЁрЂйЕБSЁїCPQЃН![]() SЁїACDЪБЃЌ
SЁїACDЪБЃЌ
Ёр![]() ЃЈ
ЃЈ![]() tЃЉ
tЃЉ![]() ЃН
ЃН![]() ЁС
ЁС![]() ЁС
ЁС![]() ЁС
ЁС![]() ЃЌ
ЃЌ
Ёр5t224tЃЋ16ЃН0ЃЌ
Ёр![]() Лђ4ЃЎ
Лђ4ЃЎ
ЂкЕБSЁїCPDЃН![]() SЁїACDЪБЃЌ
SЁїACDЪБЃЌ
Ёр![]() ЃЈ
ЃЈ![]() tЃЉ
tЃЉ![]() ЃН
ЃН![]() ЁС
ЁС![]() ЁС
ЁС![]() ЁС
ЁС![]() ЃЌ
ЃЌ
Ёр5t224tЃЋ176ЃН0ЃЌЖјЁї2424ЁС5ЁС176ЃН5763520ЃМ0ЃЌ
ДЫЗНГЬЮоНтЃЌМДЃКДЫжжЧщПіВЛДцдкЃЌ
злЩЯЫљЪіЃЌЕБtЃН![]() Лђ4ЪБЃЌPQЗжЁїACDЕФУцЛ§ЮЊ1ЃК11ЃЎ
Лђ4ЪБЃЌPQЗжЁїACDЕФУцЛ§ЮЊ1ЃК11ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
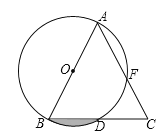
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌBDЪЧЁбOЕФЯвЃЌбгГЄBDЕНЕуCЃЌЪЙDC=BDЃЌСЌНсACНЛЁбOгкЕуFЃЎ
ЃЈ1ЃЉABгыACЕФДѓаЁгаЪВУДЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєAB=8ЃЌЁЯBAC=45ЁуЃЌЧѓЃКЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЃЈ2ЃЉЩшЗНГЬЕФСНИіЪЕЪ§ИљЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЃЌШє
ЃЉЃЌШє![]() ЪЧЙигк
ЪЧЙигк![]() ЕФКЏЪ§ЃЌЧв
ЕФКЏЪ§ЃЌЧв![]() ЃЌЧѓетИіКЏЪ§ЕФНтЮіЪНЃЛ
ЃЌЧѓетИіКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉНЋЃЈ2ЃЉжаЫљЕУЕФКЏЪ§ЕФЭМЯѓдкжБЯп![]() ЕФзѓВрВПЗжбижБЯп
ЕФзѓВрВПЗжбижБЯп![]() ЗелЃЌЭМЯѓЕФЦфгрВПЗжБЃГжВЛБфЃЌЕУЕНвЛИіаТЕФЭМЯѓЃЎЧыФуНсКЯетИіаТЕФЭМЯѓЛиД№ЃКЕБЙигк
ЗелЃЌЭМЯѓЕФЦфгрВПЗжБЃГжВЛБфЃЌЕУЕНвЛИіаТЕФЭМЯѓЃЎЧыФуНсКЯетИіаТЕФЭМЯѓЛиД№ЃКЕБЙигк![]() ЕФКЏЪ§
ЕФКЏЪ§![]() ЕФЭМЯѓгыДЫЭМЯѓгаСНИіЙЋЙВЕуЪБЃЌ
ЕФЭМЯѓгыДЫЭМЯѓгаСНИіЙЋЙВЕуЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЈжБНгаДГіД№АИЃЉЃЎ
ЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЈжБНгаДГіД№АИЃЉЃЎ
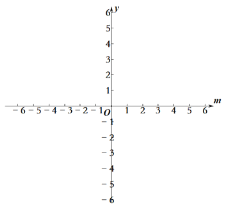
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(9Зж)вбжЊЃК![]() ABCDЕФСНБпABЃЌADЕФГЄЪЧЙигкxЕФЗНГЬ
ABCDЕФСНБпABЃЌADЕФГЄЪЧЙигкxЕФЗНГЬ![]() ЕФСНИіЪЕЪ§ИљЃЎ
ЕФСНИіЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЕБmЮЊКЮжЕЪБЃЌЫФБпаЮABCDЪЧСтаЮЃПЧѓГіетЪБСтаЮЕФБпГЄЃЛ
ЃЈ2ЃЉШєABЕФГЄЮЊ2ЃЌФЧУД![]() ABCDЕФжмГЄЪЧЖрЩйЃП
ABCDЕФжмГЄЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
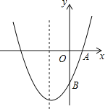
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ЕФЖдГЦжсЮЊжБЯп
ЕФЖдГЦжсЮЊжБЯп![]() ЃЌЧвО
ЃЌЧвО![]() ЁЂ
ЁЂ![]() СНЕуЃЎ
СНЕуЃЎ
![]() ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
![]() дкХзЮяЯпЕФЖдГЦжс
дкХзЮяЯпЕФЖдГЦжс![]() ЩЯЃЌЪЧЗёДцдкЕу
ЩЯЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙЫќЕНЕу
ЃЌЪЙЫќЕНЕу![]() ЕФОрРыгыЕНЕу
ЕФОрРыгыЕНЕу![]() ЕФОрРыжЎКЭзюаЁЃЌШчЙћДцдкЧѓГіЕу
ЕФОрРыжЎКЭзюаЁЃЌШчЙћДцдкЧѓГіЕу![]() ЕФзјБъЃЌШчЙћВЛДцдкЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЌШчЙћВЛДцдкЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ8ЗжЃЉШчЭМЃЌвбжЊOЪЧзјБъдЕуЃЌBЁЂCСНЕуЕФзјБъЗжБ№ЮЊЃЈ3ЃЌЃ1ЃЉЁЂЃЈ2ЃЌ1ЃЉЁЃ

ЃЈ1ЃЉвдOЕуЮЊЮЛЫЦжааФдкyжсЕФзѓВрНЋЁїOBCЗХДѓЕНСНБЖЛГіЭМаЮЁЃ
ЃЈ2ЃЉаДГіBЁЂCСНЕуЕФЖдгІЕуBЁЂCЕФзјБъЃЛ
ЃЈ3ЃЉШчЙћЁїOBCФкВПвЛЕуMЕФзјБъЮЊ(xЃЌy)ЃЌаДГіMЕФЖдгІЕуMЕФзјБъЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФДќзгжазАгаЃЈГ§беЩЋЭтЃЉЭъШЋЯрЭЌЕФКьЩЋаЁЧђ1ИіЃЌАзЩЋаЁЧђ1ИіКЭЛЦЩЋаЁЧђ2ИіЃЌ
ЃЈ1ЃЉДгжаЯШУўГівЛИіаЁЧђЃЌМЧТМЯТЫќЕФбеЩЋКѓЃЌНЋЫќЗХЛиДќжаНСдШЃЌдйУўГівЛИіаЁЧђЃЌМЧТМЯТбеЩЋ. ЧѓУўГіЕФСНИіаЁЧђЕФбеЩЋЧЁКУЪЧЁАвЛКьвЛЛЦЁБЕФИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉШчЙћУўГіЕквЛИіаЁЧђжЎКѓВЛЗХЛиДќжаЃЌдйУўГіЕкЖўИіаЁЧђЃЌетЪБУўГіЕФСНИіаЁЧђЕФбеЩЋЧЁКУЪЧЁАвЛКьвЛЛЦЁБЕФИХТЪЪЧЖрЩйЃП
ЃЈ3ЃЉаЁУїЯыИјДќжаМгШывЛаЉКьЩЋЕФаЁЧђЃЌЪЙДгДќжаШЮвтУўГівЛИіаЁЧђЧЁЮЊКьЩЋЕФИХТЪЮЊ![]() ЃЌЧыФуАяаЁУїЫувЛЫуЃЌгІИУМгШыЖрЩйИіКьЩЋЕФаЁЧђЃП
ЃЌЧыФуАяаЁУїЫувЛЫуЃЌгІИУМгШыЖрЩйИіКьЩЋЕФаЁЧђЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНУћЖгдБВЮМгЩфЛїбЕСЗЃЌУПШЫЩфЛї10ДЮЃЌГЩМЈЗжБ№ШчЯТЃК
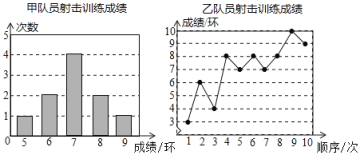
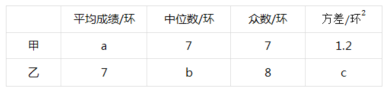
ИљОнвдЩЯаХЯЂЃЌећРэЗжЮіЪ§ОнШчЯТЃК
ЃЈ1ЃЉЬюПеЃКaЃНЁЁЁЁЃЛbЃНЁЁЁЁЃЛcЃНЁЁЁЁЃЛ
ЃЈ2ЃЉДгЦНОљЪ§КЭжаЮЛЪ§ЕФНЧЖШРДБШНЯЃЌГЩМЈНЯКУЕФЪЧЁЁЁЁЃЛЃЈЬюЁАМзЁБЛђЁАввЁБЃЉ
ЃЈ3ЃЉШєашДгМзЁЂввСНУћЖгдБжабЁдёвЛШЫВЮМгБШШќЃЌФуШЯЮЊбЁЫИќМгКЯЪЪЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкМзЁЂввСНИіВЛЭИУїЕФВМДќЃЌМзДќжазАга3ИіЭъШЋЯрЭЌЕФаЁЧђЃЌЗжБ№БъгаЪ§зж0ЃЌ1ЃЌ2ЃЛввДќжазАга3ИіЭъШЋЯрЭЌЕФаЁЧђЃЌЗжБ№БъгаЪ§зжЉ1ЃЌЉ2ЃЌ0ЃЛЯжДгМзДќжаЫцЛњГщШЁвЛИіаЁЧђЃЌМЧТМБъгаЕФЪ§зжЮЊxЃЌдйДгввДќжаЫцЛњГщШЁвЛИіаЁЧђЃЌМЧТМБъгаЕФЪ§зжЮЊyЃЌШЗЖЈЕуMзјБъЮЊЃЈxЃЌyЃЉЃЎ
ЃЈ1ЃЉгУЪїзДЭМЛђСаБэЗЈСаОйЕуMЫљгаПЩФмЕФзјБъЃЛ
ЃЈ2ЃЉЧѓЕуMЃЈxЃЌyЃЉдкКЏЪ§yЃНЉx+1ЕФЭМЯѓЩЯЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com