
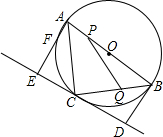
 如图,AB是⊙O的直径,直线l与⊙O相切于点C,AE⊥l交直线l于点E、交⊙O于点F,BD⊥l交直线l于点D.
如图,AB是⊙O的直径,直线l与⊙O相切于点C,AE⊥l交直线l于点E、交⊙O于点F,BD⊥l交直线l于点D.分析 (1)根据AB是⊙O的直径得到∠ACB=90°,从而得到∠BCD+∠ACE=180°-∠ACB=90°,最后得到∠BCD=∠EAC,从而利用两角对应相等的三角形是相似三角形证得△AEC∽△CDB;
(2)连结BF、OC,首先证得四边形BDEF是矩形,从而得到OC=$\frac{1}{2}$(AE+EF),然后根据OC=$\frac{1}{2}$AB得到AE+EF=AB;
(3)首先表示出AP=2t,BQ=t和BP=10-2t,然后分当BP=BQ、PB=PQ、BQ=PQ三种情况分类讨论即可求得t的值.
解答 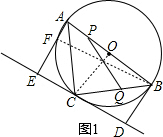 (1)证明:∵AB是⊙O的直径,
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCD+∠ACE=180°-∠ACB=90°,
∵AE⊥DE,BD⊥DE,
∴∠AEC=∠BDC=90°,
∴∠ACE+∠EAC=90°,
∴∠BCD=∠EAC,
∴△AEC∽△CDB;
(2)证明:如图1,连结BF、OC,
∵DE切⊙O于点C,
∴OC⊥DE,
又∵AE⊥DE,BD⊥DE,
∴OC∥BD∥AE,
又∵O是AB的中点,
∴OC是梯形ABDE的中位线,
∴OC=$\frac{1}{2}$(BD+AE),
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠BFE=90°,
又∵∠AED=∠BDE=90°,
∴四边形BDEF是矩形,
∴BD=FE,
∴AE+EF=AE+BD,
∴OC=$\frac{1}{2}$(AE+EF),
∵OC=$\frac{1}{2}$AB,
∴AE+EF=AB;
(3)解:由题意可知:AP=2t,BQ=t,0<t≤5,
∵∠ACB=90°,AC=8,BC=6,
∴AB=10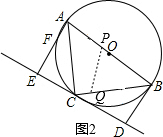 ,
,
∴BP=10-2t,
①当BP=BQ时,如图2,
10-2t=t,
t=$\frac{10}{3}$;
②当PB=PQ时,过点P作PG⊥BC于点G,如图3,
∵PB=PQ,PG⊥BC,
∴BG=$\frac{1}{2}$BQ=$\frac{1}{2}$t,∠PGB=90,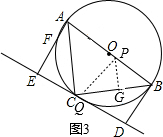
∴∠ACB=∠PGB=90°,
又∵∠PBG=∠ABC,
∴△BPG∽△BAC,
∴BP:BA=BG:BC,
∴10-2t:10=$\frac{1}{2}$t:6,
∴t=$\frac{60}{17}$;
③当BQ=PQ时,过点Q作QH⊥AB于点H,如图4,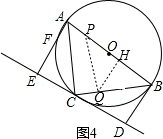 同理可求得:BH=$\frac{1}{2}$BP=$\frac{1}{2}$(10-2t)=5-t,
同理可求得:BH=$\frac{1}{2}$BP=$\frac{1}{2}$(10-2t)=5-t,
△QHB∽△ACB,
∴BH:BC=BQ:AB,
∴$\frac{5-t}{6}$=$\frac{t}{10}$,
∴t=$\frac{25}{8}$,
综上所述,当t=$\frac{10}{3}$或t=$\frac{60}{17}$或t=$\frac{25}{8}$时,△BPQ为等腰三角形.
点评 本题考查了圆的综合知识、相似三角形的判定及等腰三角形的性质,题目中还渗透了分类讨论的数学思想,是中考的热点考题之一,应加强有关的此类题目的训练.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0组 | B. | 1组 | C. | 2组 | D. | 3组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
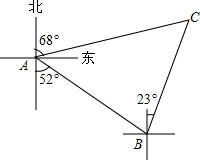 如图,某轮船航行至A处测得灯塔C位于北偏东68°的方向上,若该轮船从A处以每小时18海里的速度沿南偏东52°方向匀速航行,1小时候到达码头B,此时测得灯塔C位于北偏东23°方向上.
如图,某轮船航行至A处测得灯塔C位于北偏东68°的方向上,若该轮船从A处以每小时18海里的速度沿南偏东52°方向匀速航行,1小时候到达码头B,此时测得灯塔C位于北偏东23°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.27×109 | B. | 92.7×108 | C. | 9.27×1010 | D. | 0.927×1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com