
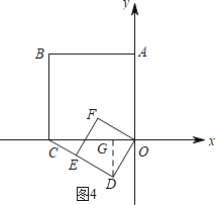
【题目】如图:正方形OABC置于坐标系中,B的坐标是(-4,4),点D是边OA上一动点,以OD为边在第一象限内作正方形ODEF.
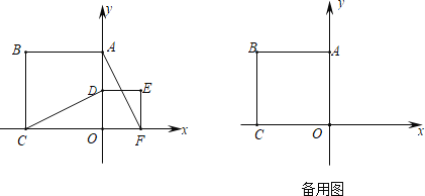
(1)CD与AF有怎样的位置关系,猜想并证明;
(2)当OD=______时,直线CD平分线段AF;
(3)在OD=2时,将正方形ODEF绕点O逆时针旋转α°(0°<α°<180°),求当C、D、E共线时D的坐标.
【答案】(1)CD⊥AF,理由见解析;(2)4![]() -4;(3)(-1,
-4;(3)(-1,![]() )或(-1,-
)或(-1,-![]() ).
).
【解析】
(1)证明△COD![]() △AOF,可得∠OCD=∠OAF,根据三角形的内角和定理可得:∠AGD=∠DOC=90°,从而得结论;
△AOF,可得∠OCD=∠OAF,根据三角形的内角和定理可得:∠AGD=∠DOC=90°,从而得结论;
(2)如图2,根据线段垂直平分线的性质得:AC=CF,列方程可得结论;
(3)分两种情况:①如图3,当D在第二象限时,过D作DG⊥x轴于G,根据直角三角形30度角的性质可得DG和OG的长,由此得D的坐标;
②如图4,当D在第三象限时,同理可得结论.
解:(1)CD⊥AF,理由是:
如图1,延长CD交AF于G,
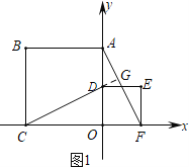
∵四边形OABC和ODEF是正方形,
∴AO=OC,∠COD=∠AOF=90°,OF=OD,
∴△COD![]() △AOF(SAS),
△AOF(SAS),
∴∠OCD=∠OAF,
∵∠ADG=∠CDO,
∴∠AGD=∠DOC=90°,
∴CD⊥AF;
(2)设OD=x,连接AC,如图2,
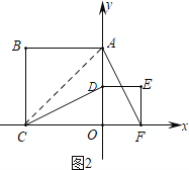
当直线CD平分线段AF时,AC=CF,
∵B的坐标是(-4,4),
∴AC=4![]() ,
,
∴4![]() =4+x,
=4+x,
x=4![]() -4,
-4,
则当OD=4![]() -4时,直线CD平分线段AF;
-4时,直线CD平分线段AF;
故答案为:4![]() -4;
-4;
(3)分两种情况:
①如图3,当D在第二象限时,过D作DG⊥x轴于G,
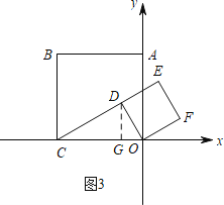
∵C、D、E共线,
∴∠CDO=∠ODE=90°,
Rt△ODC中,OD=2,OC=4,
∴∠OCD=30°,CD=2![]() ,
,
∴DG=![]() CD=
CD=![]() ,CG=3,
,CG=3,
∴OG=4-3=1,
∴D(-1,![]() ),
),
②如图4,当D在第三象限时,过D作DG⊥x轴于G,
同理得:OG=1,DG=![]() ,
,
∴D(-1,-![]() ),
),
综上,点D的坐标为:(-1,![]() )或(-1,-
)或(-1,-![]() ).
).


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,其中
,其中![]() .
.
(1)若点![]() 在y1的图象上.求a的值:
在y1的图象上.求a的值:
(2)当![]() 时.若函数有最大值2.求y1的函数表达式;
时.若函数有最大值2.求y1的函数表达式;
(3)对于一次函数![]() ,其中
,其中![]() ,若对- -切实数x,
,若对- -切实数x,![]() 都成立,求a,m需满足的数量关系及 a的取值范围.
都成立,求a,m需满足的数量关系及 a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
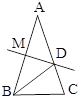
【题目】如图,已知AB=AC,∠A=36°,AB的中垂线MD交AC于点D,交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③DC+BC=AB,正确的有( )
A.3个B.2个C.1个D.0 个
查看答案和解析>>
科目:初中数学 来源: 题型:
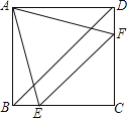
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②BD=1+![]() ;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G.

(1)判断四边形DEFG的形状,并说明理由;
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )

A.AB=CDB.AB∥CDC.∠A=∠CD.BC=AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:
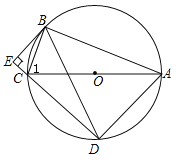
(1)∠1=∠BAD;
(2)BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店老板准备购买A、B两种型号的足球共100只,已知A型号足球进价每只40元,B型号足球进价每只60元.
(1)若该店老板共花费了5200元,那么A、B型号足球各进了多少只;
(2)若B型号足球数量不少于A型号足球数量的![]() ,那么进多少只A型号足球,可以让该老板所用的进货款最少?
,那么进多少只A型号足球,可以让该老板所用的进货款最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com