
����Ŀ����1��ij�̳���2800Ԫ�ӳ��ҹ���A��B���ּ���Ʒ��50��������A�ּ���Ʒ����Ϊÿ��80Ԫ��B�ּ���Ʒ����Ϊÿ��40Ԫ����A��B���ּ���Ʒ���������ټ���
��2���̳�Ҫ�ٴι���A��B���ּ���Ʒ��200���������۲��䣬��A�ּ���Ʒ��ÿ��110Ԫ�۳���B�ּ���Ʒ��ÿ��55Ԫ�۳����ڹ�����Щ����Ʒ���ʽ���12120Ԫ����������Щ����Ʒ����������4500Ԫ������£����̳����м��ֽ���������
��һһд��.
���𰸡���1��A�ּ���Ʒ����20����B�ּ���Ʒ����30������2���̳�����4�ֽ������������Ƿֱ��ǣ��ٹ���A�ּ���Ʒ100����B�ּ���Ʒ100�����ڹ���A�ּ���Ʒ101����B�ּ���Ʒ99�����۹���A�ּ���Ʒ102����B�ּ���Ʒ98�����ܹ���A�ּ���Ʒ103����B�ּ���Ʒ97��.
��������
��1����A��B���ּ���Ʒ�ֱ�x����y�����������ж�Ԫһ�η�������⣻��2���蹺��A�ּ���Ʒm������B�ּ���Ʒ![]() ���������ܳɱ�=���ۡ�������������Ϲ�����Щ����Ʒ���ʽ���12120Ԫ��������=�������������������������ּ���Ʒȫ���۳����ܻ���������4500Ԫ�����ɵó�����m��һԪһ�β���ʽ�飬��⼴�ɵó����ۣ�
���������ܳɱ�=���ۡ�������������Ϲ�����Щ����Ʒ���ʽ���12120Ԫ��������=�������������������������ּ���Ʒȫ���۳����ܻ���������4500Ԫ�����ɵó�����m��һԪһ�β���ʽ�飬��⼴�ɵó����ۣ�
��1����A��B���ּ���Ʒ�ֱ�x����y�����������
![]()
���![]()
��A�ּ���Ʒ����20����B�ּ���Ʒ����30��.
��2���蹺��A�ּ���Ʒm������B�ּ���Ʒ![]() �����������
�����������
![]()
�ⲻ��ʽ���![]()
![]() ������
������
![]() ��101��102��103
��101��102��103
���̳�����4�ֽ������������Ƿֱ��ǣ�
�ٹ���A�ּ���Ʒ100����B�ּ���Ʒ100����
�ڹ���A�ּ���Ʒ101����B�ּ���Ʒ99����
�۹���A�ּ���Ʒ102����B�ּ���Ʒ98����
�ܹ���A�ּ���Ʒ103����B�ּ���Ʒ97��.


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ����Ϊ������̬������A��B������������������������������Ͳ������䣬ÿ��μ������������ܿ�֧���±���

��1������������ͬ����ߵ��˾�֧������һ������������������Ͳ���������˾�֧�����ø��Ƕ���Ԫ��
��2�����˾�֧�����ò��������£�Ϊ��Լ��֧��������Э��40�˹�ͬ������������Ͳ������䣮Ҫʹ��֧��������102000Ԫ��������������������С�������������������������ļ��ַ���������Ա������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������˾Ϊ���������Լ�õ磬��ȡ�����õ����ֶ��շѰ취����ij������ÿ��Ӧ�����y��Ԫ�����õ���x���ȣ��ĺ���ͼ����һ�����ߣ���ͼ��ʾ��������ͼ����������⣺
(1) �ֱ�д����0��x��100��x��100ʱ��y��x�ĺ�����ϵʽ
(2) ���ú�����ϵʽ��˵��������˾��ȡ���շѱ�
(3) �����û�ij���õ�62�ȣ���Ӧ�ɷѶ���Ԫ�������û�ij�½ɷ�105Ԫʱ������û��������˶��ٶȵ磿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ���ҵ�
���ҵ�![]() ������Ϊ
������Ϊ![]() ����
����![]() Ϊ
Ϊ![]() ���е�.
���е�.
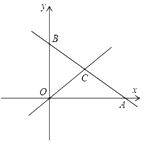
��1����![]() ��������________����
��������________����![]() ��������________;
��������________;
��2��ֱ��![]() ����һ��
����һ��![]() ����
����![]() ���������
���������![]() �����ꣻ
�����ꣻ
��3������![]() Ϊֱ��
Ϊֱ��![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() ��
��![]() ��Ĵ��ߣ���ֱ��
��Ĵ��ߣ���ֱ��![]() ���ڵ�
���ڵ�![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ���߶�
���߶�![]() �ij���Ϊ
�ij���Ϊ![]() ����
����![]() ��
��![]() �ĺ�������ʽ.
�ĺ�������ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
��ͼ��һֻ�׳���5��5�ķ���ÿ������߳���Ϊ1�����������������У������ǹ涨������ͼ�����У����ϣ������ң����м�Ϊ��+�������£����������м�Ϊ�����������ҵ�һ������ʾ���ҷ��ڶ�������ʾ���·���
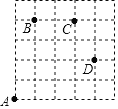
���磺��A��B��Ϊ��A��B��+1��+4������D��C��Ϊ��D��C����1��+2����
˼����Ӧ�ã�
��1��ͼ��B��C����������C��D��������������
��2�����׳��A��P������·������Ϊ����+3��+2������+1��+3������+1����2��������ͼ�б��P��λ�ã�
��3�����׳������·��ΪA����+1��+4������+2��0������+1����2��������4����2���������ü׳��߹�����·��S��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
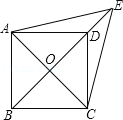
����Ŀ����ͼ����֪ƽ���ı���ABCD�У��Խ���AC��BD���ڵ�O��E��BD�ӳ����ϵĵ㣬�ҡ�ACE�ǵȱ������Σ�
��1����֤���ı���ABCD�����Σ�
��2������AED=2��EAD����֤���ı���ABCD�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
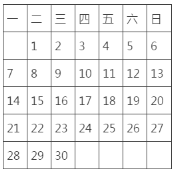
����Ŀ����ͼ����ij��11������
��1����һ���������ڱ��������ס4��������������С�ļ�Ϊ![]() ���������������ú�
���������������ú�![]() ��ʽ�ӱ�ʾ��������С��������Ϊ____________,_____________,_______________��
��ʽ�ӱ�ʾ��������С��������Ϊ____________,_____________,_______________��
��2���ڣ�1���б���ס��4����֮�͵���76ʱ����ס��4�����ֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
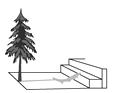
����Ŀ������������С�����һ����Ϊ1 m����͵�Ӱ��Ϊ0.4 m.
(1)��ͬһʱ��2 m����͵�Ӱ����
(2)ͬһʱ��С���ڲ������ĸ߶�ʱ����������Ӱ�Ӳ�ȫ���ڵ���������һ�������ڲٳ��ĵ�һ��̨��������ͼ��������ڵ�һ��̨���ϵ�Ӱ�ӳ�Ϊ0.1 m����һ��̨�ĸ�Ϊ0.3 m�����ڵ����ϵ�Ӱ�ӳ�Ϊ4.3 m�������ĸ߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� ��ͼ��1����ֱ��l����2���㣬��ͼ����2������ͼ����ĸ��ʾ�����ߣ�A1A2��A2A1����1���߶Σ�A1A2��
�� ��ͼ��2����ֱ��l����3���㣬��ͼ���м�������ͼ����ĸ��ʾ�����ߣ��м����߶Σ����ֱ���ͼ����ĸ��ʾ������
�� ��ͼ��3����ֱ��l����n���㣬��ͼ���ж���������ͼ����ĸ��ʾ�����ߣ��ж������߶Σ��ֱ��ú�n�Ĵ���ʽ��ʾ������
�� Ӧ�ã�3���з��ֵĹ��ɽ�����⣺ijУ���꼶����8����������������������ѭ��������ÿ����֮����һ������Ԥ��ȫ�����깲����ٳ�������
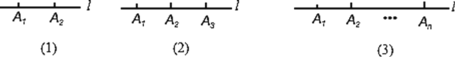
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com