
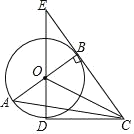
【题目】如图,AB是⊙O的直径,过点B做⊙O的切线BC,点D为⊙O上一点,且CD=CB,连结DO并延长交CB的延长线于点E.
(1)求证:CD是⊙O的切线;
(2)连接AC,若BE=4,DE=8,求线段AC的长.
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC摆放在平面直角坐标系![]() 中,点A在
中,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,OA=8,OC=6.
轴上,OA=8,OC=6.


(1)求直线AC的表达式
(2)若直线![]() 与矩形OABC有公共点,求
与矩形OABC有公共点,求![]() 的取值范围;
的取值范围;
(3)若点O与点B位于直线![]() 两侧,直接写出
两侧,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
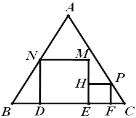
【题目】如图,正三角形ABC的边长为3+![]() ,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
A. ![]() B.
B. ![]() C. 3D.
C. 3D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数![]() 的图像与x轴的一个交点为O(0,0),点P(m,0)是x轴正半轴上的一个动点.
的图像与x轴的一个交点为O(0,0),点P(m,0)是x轴正半轴上的一个动点.
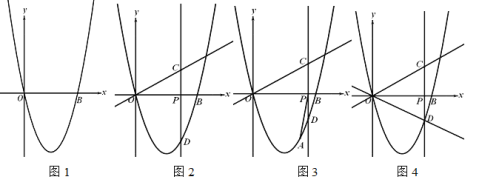
(1)如图1,求二次函数的图像与x轴另一个交点的坐标;
(2)如图2,过点P作x轴的垂线交直线![]() 与点C,交二次函数图像于点D,
与点C,交二次函数图像于点D,
①当PD=2PC时,求m的值;
如图3,已知A(3,-3)在二次函数图像上,连结AP,求![]() 的最小值;
的最小值;
(3如图4,在第(2)小题的基础上,作直线OD,作点C关于直线OD的对称点C’,当C’落在坐标轴上时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的![]() 和点P,给出如下定义:如果在
和点P,给出如下定义:如果在![]() 上存在一个动点Q,使得
上存在一个动点Q,使得![]() 是以CQ为底的等腰三角形,且满足底角
是以CQ为底的等腰三角形,且满足底角![]() ,那么就称点P为
,那么就称点P为![]() 的“关联点”.
的“关联点”.
![]() 当
当![]() 的半径为2时,
的半径为2时,
![]() 在点
在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的“关联点”是______;
的“关联点”是______;
![]() 如果点P在射线
如果点P在射线![]() 上,且P是
上,且P是![]() 的“关联点”,求点P的横坐标m的取值范围.
的“关联点”,求点P的横坐标m的取值范围.
![]() 的圆心C在x轴上,半径为4,直线
的圆心C在x轴上,半径为4,直线![]() 与两坐标轴交于A和B,如果线段AB上的点都是
与两坐标轴交于A和B,如果线段AB上的点都是![]() 的“关联点”,直接写出圆心C的横坐标n的取值范围.
的“关联点”,直接写出圆心C的横坐标n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线
y=-x2+bx+c的图象经过点A(m,0)、B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
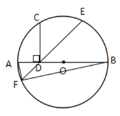
【题目】如图,AB是![]() 的直径,点D是半径OA的中点,过点D作CD⊥AB,交
的直径,点D是半径OA的中点,过点D作CD⊥AB,交![]() 于点C,点E为弧BC的中点,连结ED并延长ED交
于点C,点E为弧BC的中点,连结ED并延长ED交![]() 于点F,连结AF、BF,则( )
于点F,连结AF、BF,则( )
A. sin∠AFE=![]() B. cos∠BFE=
B. cos∠BFE=![]() C. tan∠EDB=
C. tan∠EDB=![]() D. tan∠BAF=
D. tan∠BAF=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了40m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(结果精确到1m)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com