
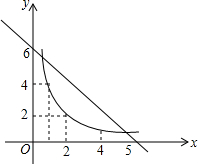
 已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?
已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?分析 设所求矩形的长为x、宽为y,表示出有关周长和面积的两个函数关系式,画出函数的图象,利用函数的图形判断是否存在这样的矩形即可.
解答 解:存在,
设所求矩形的长为x、宽为y,
∵已知矩形的长和宽分别是2和1,新矩形的周长和面积分别是已知矩形周长和面积的2倍,
∴2(x+y)=2×2×(2+1),xy=2×2×1
∴y=-x+6,y=$\frac{4}{x}$,
画出函数的图象如图,
根据图象知函数的图象有交点,所以存在两个矩形,能使得新矩形是原矩形的周长与面积的2倍.
点评 本题考查了反比例函数的应用,解题的关键是会灵活的运用函数图象交点的意义,以及图象的特点,试题中贯穿了方程思想和数形结合的思想,请注意体会.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:选择题
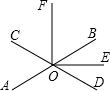 如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )
如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )| A. | 50° | B. | 75° | C. | 65° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 大桥名称 | 舟山跨海大桥 | 杭州湾跨海大桥 |
| 大桥长度 | 48千米 | 36千米 |
| 过桥费 | 100元 | 80元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com