
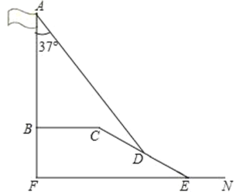
【题目】在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度,如图,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡CE的坡角为30°,旗杆的高度约为多少米?(结果精确到0.1,参考数据:sin37°=0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
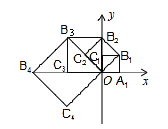
【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…则正方形OB2015B2016C2016的顶点B2016的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
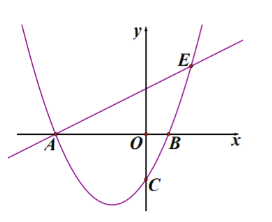
【题目】在平面直角坐标系xOy中,抛物线y=ax2+4x+c(a≠0)经过点A(3,﹣4)和B(0,2).
(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线x=3翻折,得到图象N.若过点C(9,4)的直线y=kx+b与图象M、图象N都相交,且只有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
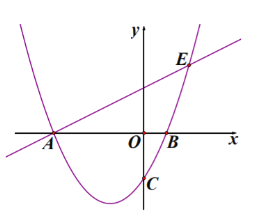
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线的另一个点为点
交抛物线的另一个点为点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
![]() 求
求![]() 和
和![]() 的值.
的值.
![]() 点
点![]() 在直线
在直线![]() 下方的抛物线上任一点,点
下方的抛物线上任一点,点![]() 的横坐标为
的横坐标为![]() 过点
过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() 设
设![]() 求出
求出![]() 与
与![]() 的函数关系式,并直接写出
的函数关系式,并直接写出![]() 的取值范围.
的取值范围.
![]() 在
在![]() 问的条件下,过点
问的条件下,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,若
,若![]() 把
把![]() 分 成面积比为
分 成面积比为![]() 的两个三角形,求出此时
的两个三角形,求出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,函数图象![]() 上点
上点![]() 的横坐标
的横坐标![]() 与其纵坐标
与其纵坐标![]() 的和
的和![]() 称为点
称为点![]() 的“坐标和”,而图象
的“坐标和”,而图象![]() 上所有点的“坐标和”中的最小值称为图象
上所有点的“坐标和”中的最小值称为图象![]() 的“智慧数”.如图:抛物线
的“智慧数”.如图:抛物线![]() 上有一点
上有一点![]() ,则点
,则点![]() 的“坐标和”为6,当
的“坐标和”为6,当![]() 时,该抛物线的“智慧数”为0.
时,该抛物线的“智慧数”为0.
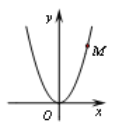
(1)点![]() 在函数
在函数![]() 的图象上,点
的图象上,点![]() 的“坐标和”是 ;
的“坐标和”是 ;
(2)求直线![]() 的“智慧数”;
的“智慧数”;
(3)若抛物线![]() 的顶点横、纵坐标的和是2,求该抛物线的“智慧数”;
的顶点横、纵坐标的和是2,求该抛物线的“智慧数”;
(4)设抛物线![]() 顶点的横坐标为
顶点的横坐标为![]() ,且该抛物线的顶点在一次函数
,且该抛物线的顶点在一次函数![]() 的图象上;当
的图象上;当![]() 时,抛物线
时,抛物线![]() 的“智慧数”是2,求该抛物线的解析式.
的“智慧数”是2,求该抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )

A.30°B.35°C.40°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m,n 为常数).
(m,n 为常数).
(1)若抛物线的的对称轴为直线 x=1,且经过点(0,-1),求 m,n 的值;
(2)若抛物线上始终存在不重合的两点关于原点对称,求 n 的取值范围;
(3)在(1)的条件下,存在正实数 a,b( a<b),当 a≤x≤b 时,恰好有![]() ,请直接写出 a,b 的值.
,请直接写出 a,b 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】"桃花流水窅然去,别有天地非人间."桃花园景点2017年三月共接待游客![]() 万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加
万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com