
【题目】在平面直角坐标系中,函数图象![]() 上点
上点![]() 的横坐标
的横坐标![]() 与其纵坐标
与其纵坐标![]() 的和
的和![]() 称为点
称为点![]() 的“坐标和”,而图象
的“坐标和”,而图象![]() 上所有点的“坐标和”中的最小值称为图象
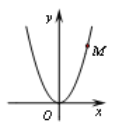
上所有点的“坐标和”中的最小值称为图象![]() 的“智慧数”.如图:抛物线
的“智慧数”.如图:抛物线![]() 上有一点
上有一点![]() ,则点
,则点![]() 的“坐标和”为6,当
的“坐标和”为6,当![]() 时,该抛物线的“智慧数”为0.
时,该抛物线的“智慧数”为0.
(1)点![]() 在函数
在函数![]() 的图象上,点
的图象上,点![]() 的“坐标和”是 ;
的“坐标和”是 ;
(2)求直线![]() 的“智慧数”;
的“智慧数”;
(3)若抛物线![]() 的顶点横、纵坐标的和是2,求该抛物线的“智慧数”;
的顶点横、纵坐标的和是2,求该抛物线的“智慧数”;
(4)设抛物线![]() 顶点的横坐标为
顶点的横坐标为![]() ,且该抛物线的顶点在一次函数
,且该抛物线的顶点在一次函数![]() 的图象上;当
的图象上;当![]() 时,抛物线
时,抛物线![]() 的“智慧数”是2,求该抛物线的解析式.
的“智慧数”是2,求该抛物线的解析式.
【答案】(1)4;(2)直线![]() “智慧数”等于
“智慧数”等于![]() ;(3)抛物线
;(3)抛物线![]() 的“智慧数”是
的“智慧数”是![]() ;(4)抛物线的解析式为
;(4)抛物线的解析式为![]() 或
或![]()
【解析】
(1)先求出点N的坐标,然后根据“坐标和”的定义计算即可;
(2)求出![]() ,然后根据一次函数的增减性和“智慧数”的定义计算即可;
,然后根据一次函数的增减性和“智慧数”的定义计算即可;
(3)先求出抛物线的顶点坐标,即可列出关于b和c的等式,然后求出![]() ,然后利用二次函数求出y+x的最小值即可得出结论;
,然后利用二次函数求出y+x的最小值即可得出结论;
(4)根据题意可设二次函数为![]() ,坐标和为
,坐标和为![]() ,即可求出
,即可求出![]() 与x的二次函数关系式,求出
与x的二次函数关系式,求出![]() 与x的二次函数图象的对称轴,先根据已知条件求出m的取值范围,然后根据
与x的二次函数图象的对称轴,先根据已知条件求出m的取值范围,然后根据![]() 与对称轴的相对位置分类讨论,分别求出
与对称轴的相对位置分类讨论,分别求出![]() 的最小值列出方程即可求出结论.
的最小值列出方程即可求出结论.
解:(1)将y=2代入到![]() 解得x=2
解得x=2
∴点N的坐标为(2,2)
∴点![]() 的“坐标和”是2+2=4
的“坐标和”是2+2=4
故答案为:4;
(2)![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 最小,
最小,
即直线![]() ,“智慧数”等于
,“智慧数”等于![]()
(3)抛物线的顶点坐标为![]() ,
,
∴![]() ,即
,即![]()
![]()
∵![]() ,
,
∴![]() 的最小值是
的最小值是![]()
∴抛物线![]() 的“智慧数”是
的“智慧数”是![]() ;
;
(4)∵二次函数![]() 的图象的顶点在直线
的图象的顶点在直线![]() 上,
上,
∴设二次函数为![]() ,坐标和为
,坐标和为![]()
![]()
对称轴![]()
∵![]()
∴![]()
①当![]() 时,即
时,即![]() 时,“坐标和”随
时,“坐标和”随![]() 的增大而增大
的增大而增大
∴把![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
当![]() 时,
时,![]()
②当![]() ,即
,即![]() 时,
时,
![]() ,即
,即![]() ,
,
解得![]() ,
,
当![]() 时,
时,![]()
③当![]() 时,
时,![]()
∵![]() ,所以此情况不存在
,所以此情况不存在
综上,抛物线的解析式为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m,![]() 分别用
分别用![]() 、
、![]() 、
、![]() 表示
表示![]() ;田赛项目:跳远,跳高
;田赛项目:跳远,跳高![]() 分别用
分别用![]() 、
、![]() 表示
表示![]() .
.
![]() 该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
![]() 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小华设计的“作一个角等于已知角的2倍”的尺规作图过程.
已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
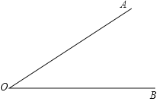
作法:如图,
①在射线![]() 上任取一点
上任取一点![]() ;
;
②作线段![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;
;
③连接![]() ;
;
所以![]() 即为所求作的角.
即为所求作的角.
根据小华设计的尺规作图过程,
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明(说明:括号里填写推理的依据).
证明:∵![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() ______(______)
______(______)
∴![]() .
.
∵![]() (______)
(______)
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,![]() .线段
.线段![]() 与线段
与线段![]() 存在一种变换关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标为__________.
存在一种变换关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
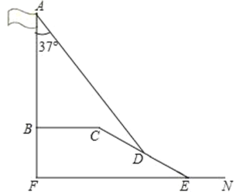
【题目】在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度,如图,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡CE的坡角为30°,旗杆的高度约为多少米?(结果精确到0.1,参考数据:sin37°=0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从 4 名女班干部(小悦、小文、小雅和小宇)中通过抽签方式确定 2 名女生去参加.抽签规则:将 4 名女班干部姓名分别写在 4 张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的 3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小安被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小文被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小雅被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
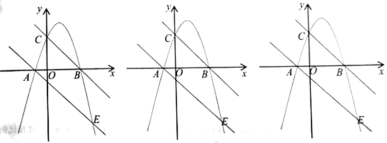
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,抛物线与直线
,抛物线与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的解析式;
(2)坐标轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形?若存在,请直接写出点
为底边的等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)![]() 点在
点在![]() 轴上且位于点
轴上且位于点![]() 的左侧,若以
的左侧,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
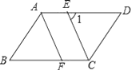
【题目】如图,在ABCD中,CE平分∠BCD,且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠B=52°,求∠1的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com