
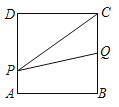
【题目】如图,边长为2的正方形ABCD,点P从点A出发以每秒1个单位长度的速度沿A﹣D﹣C的路径向点C运动,同时点Q从点B出发以每秒2个单位长度的速度沿B﹣C﹣D﹣A的路径向点A运动,当Q到达终点时,P停止移动,设△PQC的面积为S,运动时间为t秒,则能大致反映S与t的函数关系的图象是( )
A.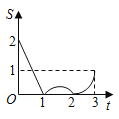 B.
B.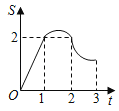
C.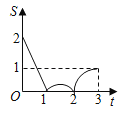 D.
D.
科目:初中数学 来源: 题型:
【题目】“端午节”是我国流传了上千年的传统节日,全国各地举行了丰富多彩的纪念活动,为了继承传统,减缓学生考前的心理压力,某班学生组织了一次拔河比赛,裁判员让两队队长用“石头、剪刀、布”的手势方式选择场地位置,规则是:石头胜剪刀,剪刀胜布,布胜石头,手势相同则再决胜负.
(1)用列表或画树状图法,列出甲、乙两队手势可能出现的情况;
(2)裁判员的这种做法对甲、乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
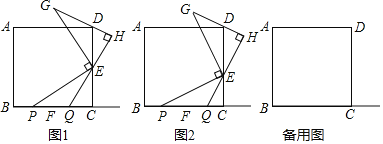
【题目】综合与实践
如图,点![]() 是正方形
是正方形![]() 的边
的边![]() 上一点,点
上一点,点![]() 在线段
在线段![]() 上,将线段
上,将线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,交射线
,交射线![]() 于点
于点![]() .
.
探究发现
(1)如图1,若点![]() 是线段
是线段![]() 的中点,直接写出线段
的中点,直接写出线段![]() 的数量关系为______;
的数量关系为______;
(2)如图2,若点![]() 不是线段
不是线段![]() 的中点,线段
的中点,线段![]() 的数量关系为______,填写出证明过程;
的数量关系为______,填写出证明过程;
(3)当![]() ,
,![]() 时,连接
时,连接![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
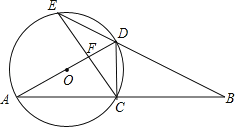
【题目】如图,以AD为直径的⊙O交AB于C点,BD的延长线交⊙O于E点,连CE交AD于F点,若AC=BC.
(1)求证:![]() ;
;
(2)若![]() ,求tan∠CED的值.
,求tan∠CED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法。
问题提出:求边长分别为![]() 的三角形面积。
的三角形面积。
问题解决:在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为![]() 的格点三角形△ABC(如图①),AB=
的格点三角形△ABC(如图①),AB=![]() 是直角边为1和2的直角三角形斜边,BC=
是直角边为1和2的直角三角形斜边,BC=![]() 是直角边分别为1和3的直角三角形的斜边,AC=
是直角边分别为1和3的直角三角形的斜边,AC=![]() 是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
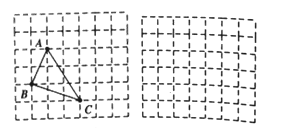
(1)请直接写出图①中△ABC的面积为_______________ 。
(2)类比迁移:求边长分别为![]() 的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问:
(1)应将每件售价定为多少元时,才能使每天利润为640元?
(2)店主想要获得每天800元的利润,小红同学认为不可能,如果你同意小红同学的说法,请进行说明;如果你不同意,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
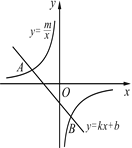
【题目】如图,已知A(-4,2)、B(n,-4)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1) 求反比例函数和一次函数的解析式;
(2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com