
ΓΨΧβΡΩΓΩΡ≥…ΧΒξΫΪΫχΦέΈΣ8‘ΣΒΡ…ΧΤΖΑ¥ΟΩΦΰ10‘Σ έ≥ωΘ§ΟΩΧλΩ… έ≥ω200ΦΰΘ§œ÷‘Ύ≤…»ΓΧαΗΏ…ΧΤΖ έΦέΦθ…Όœζ έΝΩΒΡΑλΖ®‘ωΦ”άϊ»σΘ§»γΙϊ’β÷÷…ΧΤΖΟΩΦΰΒΡœζ έΦέΟΩΧαΗΏ0.5‘ΣΤδœζ έΝΩΨΆΦθ…Ό10ΦΰΘ§Έ ΘΚ
(1)”ΠΫΪΟΩΦΰ έΦέΕ®ΈΣΕύ…Ό‘Σ ±Θ§≤≈Ρή ΙΟΩΧλάϊ»σΈΣ640‘ΣΘΩ
(2)Βξ÷ςœκ“ΣΜώΒΟΟΩΧλ800‘ΣΒΡάϊ»σΘ§–ΓΚλΆ§―ß»œΈΣ≤ΜΩ…ΡήΘ§»γΙϊΡψΆ§“β–ΓΚλΆ§―ßΒΡΥΒΖ®Θ§«κΫχ––ΥΒΟςΘΜ»γΙϊΡψ≤ΜΆ§“βΘ§«κΦρ“ΣΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΟΩΦΰ έΦέΕ®ΈΣ12‘ΣΜρ16‘ΣΘΜΘ®2Θ©Ά§“β–ΓΚλΆ§―ßΒΡΥΒΖ®Θ§ΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ© Ήœ»…ηΫΪΟΩΦΰ…ΧΤΖΧαΦέx‘ΣΘ§‘ρΟΩΧλΩ… έ≥ωΗΟ…ΧΤΖ(200Θ≠![]() )ΦΰΘ§»ΜΚσΗυΨίΧβ“βΝ–≥ωΖΫ≥ΧΘ§Φ¥Ω…ΒΟΫβΘΜ
)ΦΰΘ§»ΜΚσΗυΨίΧβ“βΝ–≥ωΖΫ≥ΧΘ§Φ¥Ω…ΒΟΫβΘΜ
Θ®2Θ© Ήœ»…ηΫΪΟΩΦΰ…ΧΤΖΧαΦέy‘ΣΘ§‘ρΟΩΧλΩ… έ≥ωΗΟ…ΧΤΖ(200Θ≠![]() )ΦΰΘ§»ΜΚσΗυΨίΧβ“βΝ–≥ωΖΫ≥ΧΘ§”…ΗυΒΡ≈–±π ΫΒΟ≥ωΖΫ≥ΧΈόΫβΘ§Φ¥Ω…ΒΟΫβ.
)ΦΰΘ§»ΜΚσΗυΨίΧβ“βΝ–≥ωΖΫ≥ΧΘ§”…ΗυΒΡ≈–±π ΫΒΟ≥ωΖΫ≥ΧΈόΫβΘ§Φ¥Ω…ΒΟΫβ.
(1)…ηΫΪΟΩΦΰ…ΧΤΖΧαΦέx‘ΣΘ§‘ρΟΩΧλΩ… έ≥ωΗΟ…ΧΤΖ(200Θ≠![]() )ΦΰΘ§
)ΦΰΘ§
ΗυΨίΧβ“βΘ§ΒΟ(10Θ≠8ΘΪx)(200Θ≠![]() )=640Θ§
)=640Θ§
ΫβΒΟx1=2Θ§x2=6Θ°
Γύ10ΘΪx=12Μρ16Θ§
¥πΘΚΟΩΦΰ έΦέΕ®ΈΣ12‘ΣΜρ16‘ΣΘΜ
(2)Ά§“β–ΓΚλΆ§―ßΒΡΥΒΖ®Θ§άμ”…»γœ¬ΘΚ
…ηΫΪΟΩΦΰ…ΧΤΖΧαΦέy‘ΣΘ§‘ρΟΩΧλΩ… έ≥ωΗΟ…ΧΤΖ(200Θ≠![]() )ΦΰΘ§
)ΦΰΘ§
ΗυΨίΧβ“βΘ§ΒΟ(10Θ≠8ΘΪy)(200Θ≠![]() ) =800Θ§
) =800Θ§
’ϊάμΘ§ΒΟy2Θ≠8yΘΪ20=0Θ§
ΓΏΠΛ= (Θ≠8)2Θ≠4ΓΝ1ΓΝ20=Θ≠16ΘΦ0Θ§
ΓύΗΟΖΫ≥ΧΈό Β ΐΫβΘ§Φ¥–ΓΚλΒΡΥΒΖ®’ΐ»ΖΘ°


 άΦΆΑΌΆ®ΤΎΡ©ΫπΨμœΒΝ–¥πΑΗ
άΦΆΑΌΆ®ΤΎΡ©ΫπΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐyΘΫx2©¹2x©¹3”κx÷αΝΫΫΜΒψ÷°ΦδΒΡΨύάκΈΣ_____Θ°≈ΉΈοœΏΕΞΒψΓΔ”κx÷α’ΐΑκ÷αΚΆy÷αΒΡΫΜΒψΈß≥…ΒΡ»ΐΫ«–ΈΟφΜΐ «_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
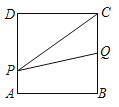
ΓΨΧβΡΩΓΩ»γΆΦΘ§±Ώ≥ΛΈΣ2ΒΡ’ΐΖΫ–ΈABCDΘ§ΒψP¥”ΒψA≥ωΖΔ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊA©¹D©¹CΒΡ¬ΖΨΕœρΒψC‘ΥΕ·Θ§Ά§ ±ΒψQ¥”ΒψB≥ωΖΔ“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊB©¹C©¹D©¹AΒΡ¬ΖΨΕœρΒψA‘ΥΕ·Θ§Β±QΒΫ¥ο÷’Βψ ±Θ§PΆΘ÷Ι“ΤΕ·Θ§…ηΓςPQCΒΡΟφΜΐΈΣSΘ§‘ΥΕ· ±ΦδΈΣtΟκΘ§‘ρΡή¥σ÷¬Ζ¥”≥S”κtΒΡΚ· ΐΙΊœΒΒΡΆΦœσ «Θ®ΓΓΓΓΘ©
A.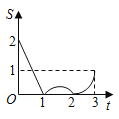 B.
B.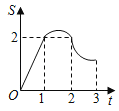
C.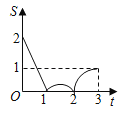 D.
D.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ“Μ¥ΈΚ· ΐ![]() ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ
ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ![]() Θ®
Θ®![]() Θ©ΒΡΆΦœσœύΫΜ”ΎAΘ§BΝΫΒψΘ®A‘ΎBΒΡ”“≤ύΘ©Θ°
Θ©ΒΡΆΦœσœύΫΜ”ΎAΘ§BΝΫΒψΘ®A‘ΎBΒΡ”“≤ύΘ©Θ°
Θ®1Θ©Β±AΘ®4Θ§2Θ© ±Θ§«σΖ¥±»άΐΚ· ΐΒΡΫβΈω ΫΦΑBΒψΒΡΉχ±ξΘΜ
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§Ζ¥±»άΐΚ· ΐΆΦœσΒΡΝμ“Μ÷ß…œ «Ζώ¥φ‘Ύ“ΜΒψPΘ§ ΙΓςPAB «“‘ABΈΣ÷±Ϋ«±ΏΒΡ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«σ≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©Β±AΘ®aΘ§©¹2a+10Θ©Θ§BΘ®bΘ§©¹2b+10Θ© ±Θ§÷±œΏOA”κ¥ΥΖ¥±»άΐΚ· ΐΆΦœσΒΡΝμ“Μ÷ßΫΜ”ΎΝμ“ΜΒψCΘ§Ν§Ϋ”BCΫΜy÷α”ΎΒψDΘ°»τ![]() Θ§«σΓςABCΒΡΟφΜΐΘ°
Θ§«σΓςABCΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
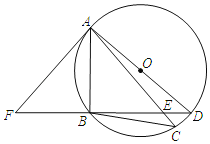
ΓΨΧβΡΩΓΩ»γΆΦΘ§AD «Γ―OΒΡ÷±ΨΕΘ§ΜΓBAΘΫΜΓBCΘ§BDΫΜAC”ΎΒψEΘ§ΒψF‘ΎDBΒΡ―”≥ΛœΏ…œΘ§«“ΓœBAFΘΫΓœCΘ°
Θ®1Θ©«σ÷ΛΘΚAF «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©«σ÷ΛΘΚΓςABEΓΉΓςDBAΘΜ
Θ®3Θ©»τBDΘΫ8Θ§BEΘΫ6Θ§«σABΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ÷±œΏy=![]() ”κx÷αΓΔy÷αΖ÷±πΫΜ”ΎAΓΔBΝΫΒψΘ§P «“‘CΘ®0Θ§2Θ©ΈΣ‘≤–ΡΘ§2ΈΣΑκΨΕΒΡ‘≤…œ“ΜΕ·ΒψΘ§Ν§ΫαPAΓΔPBΘ°‘ρΓςPABΟφΜΐΒΡΉν–Γ÷Β «_____Θ°
”κx÷αΓΔy÷αΖ÷±πΫΜ”ΎAΓΔBΝΫΒψΘ§P «“‘CΘ®0Θ§2Θ©ΈΣ‘≤–ΡΘ§2ΈΣΑκΨΕΒΡ‘≤…œ“ΜΕ·ΒψΘ§Ν§ΫαPAΓΔPBΘ°‘ρΓςPABΟφΜΐΒΡΉν–Γ÷Β «_____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡ±Ώ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ°“―÷ΣAΘ®-2Θ§0Θ©ΓΔBΘ®6Θ§0Θ©ΓΔDΘ®0Θ§3Θ©Ζ¥±»άΐΚ· ΐ
Θ°“―÷ΣAΘ®-2Θ§0Θ©ΓΔBΘ®6Θ§0Θ©ΓΔDΘ®0Θ§3Θ©Ζ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσΨ≠ΙΐΒψ
ΒΡΆΦœσΨ≠ΙΐΒψ![]() Θ°
Θ°
Θ®1Θ©«σΒψ![]() ΒΡΉχ±ξΚΆΖ¥±»άΐΚ· ΐ
ΒΡΉχ±ξΚΆΖ¥±»άΐΚ· ΐ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΫΪΥΡ±Ώ–Έ![]() ―Ί
―Ί![]() ÷αœρ…œΤΫ“Τ
÷αœρ…œΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»ΒΟΒΫΥΡ±Ώ–Έ
ΗωΒΞΈΜ≥ΛΕ»ΒΟΒΫΥΡ±Ώ–Έ![]() Θ§Έ Βψ
Θ§Έ Βψ![]() «Ζώ¬δ‘ΎΘ®1Θ©÷–ΒΡΖ¥±»άΐΚ· ΐΒΡΆΦœσ…œΘΩ
«Ζώ¬δ‘ΎΘ®1Θ©÷–ΒΡΖ¥±»άΐΚ· ΐΒΡΆΦœσ…œΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΓςABC‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΒΡΈΜ÷Ο»γΆΦΥυ ΨΘ°«κΫβ¥πΘΚ
Θ®1Θ©ΒψAΓΔCΒΡΉχ±ξΖ÷±π «ΓΓΓΓΓΓΓΓ ΓΔΓΓΓΓΓΓΓΓ ΘΜ
Θ®2Θ©Μ≠≥ωΓςABC»ΤΒψAΑ¥Ρφ ±’κΖΫœρ–ΐΉΣ90ΓψΚσΒΡΓςAB'C'ΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§«σΒψC–ΐΉΣΒΫΒψC'ΥυΨ≠ΙΐΒΡ¬ΖœΏ≥Λ(ΫαΙϊ±ΘΝτΠ–)Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
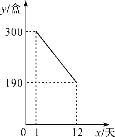
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨΩΣΖΔ≥ω“ΜΩν–¬ΑϋΉΑΒΡ≈ΘΡΧΘ§≈ΘΡΧΒΡ≥…±ΨΦέΈΣ6‘Σ/Κ–Θ§’β÷÷–¬ΑϋΉΑΒΡ≈ΘΡΧ‘Ύ’ΐ ΫΆΕΖ≈ –≥Γ«ΑΆ®Ιΐ¥ζœζΒψΫχ––ΝΥΈΣΤΎ“ΜΗω‘¬(30Χλ)ΒΡ ‘”ΣœζΘ§ έΦέΈΣ8‘Σ/Κ–Θ°«ΑΦΗΧλΒΡœζΝΩΟΩΩω”ζœ¬Θ§ΙΛΉς»Υ‘±Ε‘œζ έ«ιΩωΫχ––ΝΥΗζΉΌΦ«¬ΦΘ§≤ΔΫΪΦ«¬Φ«ιΩωΜφ≥…ΆΦœσΘ§ΆΦ÷–ΒΡœΏΕΈ±μ Ψ«Α12Χλ»’œζ έΝΩy(Κ–)”κœζ έ ±Φδx(Χλ)÷°ΦδΒΡΚ· ΐΙΊœΒΘ§”Ύ «¥”ΒΎ13ΧλΤπ≤…”Ο¥ρ’έœζ έ(≤ΜΒΆ”Ύ≥…±ΨΦέ)Θ§ ±ΦδΟΩ‘ωΦ”1ΧλΘ§»’œζ έΝΩΨΆ‘ωΦ”10Κ–Θ°
Θ®1Θ©¥ρ’έœζ έΚσΘ§ΒΎ17ΧλΒΡ»’œζ έΝΩΈΣ________Κ–ΘΜ
Θ®2Θ©«σy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©“―÷Σ»’œζ έάϊ»σ≤ΜΒΆ”Ύ560‘ΣΒΡΧλ ΐΙ≤”–6ΧλΘ§…η¥ρ’έœζ έΒΡ’έΩέΈΣa’έΘ§ ‘»ΖΕ®aΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com