
【题目】综合与探究
如图,已知抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.其顶点为D,对称轴是直线l,且与x轴交于点H.

(1)求点A,B,C,D的坐标;
(2)若点P是该抛物线对称轴l上的﹣个动点,求△PBC周长的最小值;
(3)若点E是线段AC上的一个动点(E与A.C不重合),过点E作x轴的垂线,与抛物线交于点F,与x轴交于点G.则在点E运动的过程中,是否存在EF=2EG?若存在,求出此时点E的坐标;若不存在,请说明理由.
【答案】(1)点A坐标为(﹣3,0),点B坐标为(﹣1,0).点C坐标为(0,3).点D坐标为(﹣1,4);(2)△PBC周长的最小值为![]() ;(3)存在点E(﹣2,1),使得EF=2EG.
;(3)存在点E(﹣2,1),使得EF=2EG.
【解析】
(1)当y=0时,-x2-2x+3=0,求得:点A坐标为(-3,0),点B坐标为(-1,0);令x=0,求得C坐标为(0,3);化为顶点式即可求得点D的坐标;
(2)△PBC的周长为PB+PC+BC,BC为定值,当PB+PC最小时,△PBC的周长最小.即可求解;
(3)设点E坐标为(x,x+3),点F(x,-x2-2x+3),则EF=(-x2-2x+3)-(x+3)=-x2-3x,EG=x+3,即可求解.
(1)当y=0时,﹣x2﹣2x+3=0,
解得x1=﹣3,x2=1,∴点A坐标为(﹣3,0),点B坐标为(﹣1,0).
当x=0时,y=3,∴点C坐标为(0,3).
∵y=﹣(x+1)2+4
∴点D坐标为(﹣1,4);
(2)△PBC的周长为PB+PC+BC,
∵BC为定值,∴当PB+PC最小时,△PBC的周长最小.
∵点A,点B关于抛物线的对称轴l对称,
∴连接AC,交l于点P,点P即为所求的点.
∵AP=BP,∴PB+PC+BC=AC+BC.
∵A(﹣3,0),B(﹣1,0),C(0,3),
∴AC=![]() ,BC=
,BC=![]() ,
,
∴△PBC周长的最小值为![]() ;
;

(3)设直线AC的解析式为y=kx+b,得![]() .
.
解得k=1,b=3.
∴直线AC的解析式为y=x+3.
设点E坐标为(x,x+3),点F(x,﹣x2﹣2x+3),
则EF=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x,EG=x+3.
当EF=2EG时,有﹣x2﹣3x=2(x+3).
解得x1=﹣2,x2=﹣3(舍去)
当x=﹣2时,点E坐标为(﹣2,1).
∴存在点E(﹣2,1),使得EF=2EG.


科目:初中数学 来源: 题型:
【题目】如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
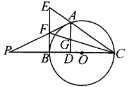
(1)求证:BF=EF;
(2)求证:PA是⊙O的切线;
(3)若FG=BF,且⊙O的半径长为3![]() ,求BD和FG的长度.
,求BD和FG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某斜拉索大桥,主索塔呈抛物线,主索塔底部在水面部分的宽度AB=50米,主索塔的最高点E距水面的垂直距离为100米,桥面CD距水面的咨度为36米,则桥的宽度CD_____米.
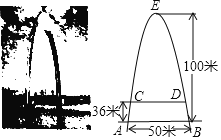
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,《九章算术》是我国古代数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:无论k为何值,方程总有实数根;
(2)若等腰△ABC的一边长为2,另两边的长为这个方程的两个实数根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用指定的方法解下列方程:
(1)4(x﹣1)2﹣36=0(直接开平方法);
(2)2x2﹣5x+1=0 (配方法)
(3)(x+1)(x﹣2)=4(公式法);
(4)2(x+1)﹣x(x+1)=0(因式分解法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 在射线
在射线![]() 上,过
上,过![]() 作
作![]() 于
于![]() ,设
,设![]() .
.
(1)求证:![]() ;
;
(2)当![]() 也是
也是![]() 边中点时,求
边中点时,求![]() 的值;
的值;
(3)若以![]() ,
,![]() ,
,![]() 为顶点的三角形也与
为顶点的三角形也与![]() 相似,试求
相似,试求![]() 的值;
的值;
(4)当点![]() 与点
与点![]() 重合时,设
重合时,设![]() 交
交![]() 于点
于点![]() ,试判断
,试判断![]() 与
与![]() 的大小关系并说明理由.
的大小关系并说明理由.
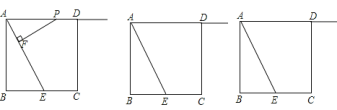
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com