
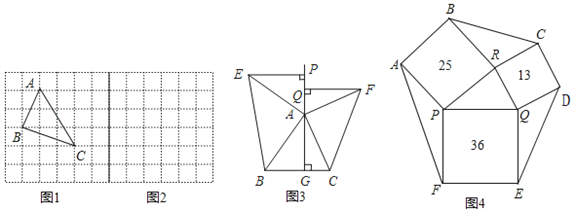
ЁОЬтФПЁПдкЁїABCжаЃЌABЁЂBCЁЂACШ§БпЕФГЄЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЧѓетИіШ§НЧаЮЕФУцЛ§ЃЎаЁЛЊЭЌбЇдкНтД№етЕРЬтЪБЃЌЯШЛвЛИіе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЉЃЌдйдкЭјИёжаЛГіИёЕуЁїABCЃЈМДЁїABCШ§ИіЖЅЕуЖМдкаЁе§ЗНаЮЕФЖЅЕуДІЃЉЃЌШчЭМ1ЫљЪОЃЎетбљВЛашЧѓЁїABCЕФИпЃЌЖјНшгУЭјИёОЭФмМЦЫуГіЫќЕФУцЛ§ЃЎетжжЗНЗЈНазіЙЙЭМЗЈЃЎ
ЃЌЧѓетИіШ§НЧаЮЕФУцЛ§ЃЎаЁЛЊЭЌбЇдкНтД№етЕРЬтЪБЃЌЯШЛвЛИіе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЉЃЌдйдкЭјИёжаЛГіИёЕуЁїABCЃЈМДЁїABCШ§ИіЖЅЕуЖМдкаЁе§ЗНаЮЕФЖЅЕуДІЃЉЃЌШчЭМ1ЫљЪОЃЎетбљВЛашЧѓЁїABCЕФИпЃЌЖјНшгУЭјИёОЭФмМЦЫуГіЫќЕФУцЛ§ЃЎетжжЗНЗЈНазіЙЙЭМЗЈЃЎ
ЃЈ1ЃЉЁїABCЕФУцЛ§ЮЊЃКЁЁ ЁЁЃЎ
ЃЈ2ЃЉШєЁїDEFШ§БпЕФГЄЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЧыдкЭМ2ЕФе§ЗНаЮЭјИёжаЛГіЯргІЕФЁїDEFЃЌВЂРћгУЙЙЭМЗЈЧѓГіЫќЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
ЃЌЧыдкЭМ2ЕФе§ЗНаЮЭјИёжаЛГіЯргІЕФЁїDEFЃЌВЂРћгУЙЙЭМЗЈЧѓГіЫќЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌЁїABCжаЃЌAGЁЭBCгкЕуGЃЌвдAЮЊжБНЧЖЅЕуЃЌЗжБ№вдABЁЂACЮЊжБНЧБпЃЌЯђЁїABCЭтзїЕШбќRtЁїABEКЭЕШбќRtЁїACFЃЌЙ§ЕуEЁЂFзїЩфЯпGAЕФДЙЯпЃЌДЙзуЗжБ№ЮЊPЁЂQЃЎЪдЬНОПEPгыFQжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
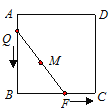
ЃЈ4ЃЉШчЭМ4ЃЌвЛИіСљБпаЮЕФЛЈЬГБЛЗжИюГЩ7ИіВПЗжЃЌЦфжае§ЗНаЮPRBAЃЌRQDCЃЌQPFEЕФУцЛ§ЗжБ№ЮЊ13m2ЁЂ25m2ЁЂ36m2ЃЌдђСљБпаЮЛЈЬГABCDEFЕФУцЛ§ЪЧЁЁ ЁЁm2ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ3.5ЃЛЃЈ2ЃЉ3ЃЛ ЃЈ3ЃЉEP=FQЃЌжЄУїМћНтЮіЃЛЃЈ4ЃЉ110mЃЎ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉРћгУЁїABCЫљдкЕФе§ЗНаЮЕФУцЛ§МѕШЅЫФжмШ§ИіаЁжБНЧШ§НЧаЮЕФУцЛ§ЃЌМЦЫуМДПЩЕУНтЃЛ
ЃЈ2ЃЉИљОнЭјИёНсЙЙКЭЙДЙЩЖЈРэзїГіЁїDEFЃЌдйРћгУЁїDEFЫљдкЕФОиаЮЕФУцЛ§МѕШЅЫФжмШ§ИіаЁжБНЧШ§НЧаЮЕФУцЛ§ЃЌМЦЫуМДПЩЕУНтЃЛЃЈ3ЃЉРћгУЭЌНЧЕФгрНЧЯрЕШЧѓГіЁЯBAG=ЁЯAEPЃЌШЛКѓРћгУЁАНЧНЧБпЁБжЄУїЁїABGКЭЁїEAPШЋЕШЃЌЭЌРэПЩжЄЁїACGКЭЁїFAQШЋЕШЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШПЩЕУEP=AG=FQЃЛЃЈ4ЃЉЙ§RзїRHЁЭPQгкHЃЌЩшPH=hЃЌдкRtЁїPRHКЭRtЁїRQHжаЃЌРћгУЙДЙЩЖЈРэСаЪНБэЪОГіPQЃЌШЛКѓНтЮоРэЗНГЬЧѓГіhЃЌДгЖјЧѓГіЁїPQRЕФУцЛ§ЃЌдйИљОнСљБпаЮБЛЗжГЩЕФЫФИіШ§НЧаЮЕФУцЛ§ЯрЕШЃЌзмУцЛ§ЕШгкИїВПЗжЕФУцЛ§жЎКЭСаЪНМЦЫуМДПЩЕУНтЃЎ
БОЬтНтЮіЃК
(1)ЁїABCЕФУцЛ§=3ЁС3![]() ЁС2ЁС1
ЁС2ЁС1![]() ЁС3ЁС1
ЁС3ЁС1![]() ЁС2ЁС3=911.53=95.5=3.5ЃЛ
ЁС2ЁС3=911.53=95.5=3.5ЃЛ
(2)ЁїDEFШчЭМ2ЫљЪО:

УцЛ§=2ЁС4![]() ЁС1ЁС2
ЁС1ЁС2![]() ЁС2ЁС2
ЁС2ЁС2![]() ЁС1ЁС4=8122=85=3ЃЛ
ЁС1ЁС4=8122=85=3ЃЛ
(3) EP=FQЃЌ
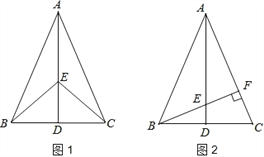
жЄУїЃКЁпЁїABEЪЧЕШбќжБНЧШ§НЧаЮЃЌЁрAB=AE,ЁЯBAE=90ЃЌ
ЁрЁЯPAE+ЁЯBAG=180Ёу90Ёу=90Ёу,гжЁпЁЯAEP+ЁЯPAE=90ЁуЃЌЁрЁЯBAG=ЁЯAEPЃЌ
дкЁїABGКЭЁїEAPжаЃЌ
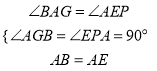 ЃЌЁрЁїABGЁеЁїEAP(AAS)ЃЌЭЌРэПЩжЄ,ЁїACGЁеЁїFAQЃЌЁрEP=AG=FQЃЛ
ЃЌЁрЁїABGЁеЁїEAP(AAS)ЃЌЭЌРэПЩжЄ,ЁїACGЁеЁїFAQЃЌЁрEP=AG=FQЃЛ
(4)ШчЭМ4ЃЌЙ§RзїRHЁЭPQгкHЃЌЩшRH=hЃЌ

дкRtЁїPRHжа,PH=![]() ЃЌ
ЃЌ
дкRtЁїRQHжа,QH=![]() ,
,
ЁрPQ=![]() =6ЃЌ
=6ЃЌ
![]() ЃЌ
ЃЌ
СНБпЦНЗНЕУ,25h=3612![]() +13hЃЌ
+13hЃЌ
ећРэЕУ, ![]() =2ЃЌ
=2ЃЌ
СНБпЦНЗНЕУ,13h=4ЃЌ
НтЕУh=3ЃЌ
Ёр![]() ЁС6ЁС3=9ЃЌ
ЁС6ЁС3=9ЃЌ
ЁрСљБпаЮЛЈЬГABCDEFЕФУцЛ§=25+13+36+4ЁС9=74+36=110m.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгазуЙЛЖрЕФГЄЗНаЮКЭе§ЗНаЮПЈЦЌЃЌШчЭМЃЎ


ЃЈ1ЃЉШчЭМЃЌШчЙћбЁШЁ1КХЁЂ2КХЁЂ3КХПЈЦЌЗжБ№ЮЊ1еХЁЂ2еХЁЂ3еХЃЌПЩЦДГЩвЛИіГЄЗНаЮ(ВЛжиЕўЮоЗьЯЖ)ЃЎЧыЛГіетИіГЄЗНаЮЕФВнЭМЃЌВЂдЫгУЦДЭМЧАКѓУцЛ§жЎМфЕФЙиЯЕЫЕУїетИіГЄЗНаЮЕФДњЪ§втвхЃЎ
етИіГЄЗНаЮЕФДњЪ§втвхЪЧ______________ЃЛ
ЃЈ2ЃЉаЁУїЯыгУРрЫЦЗНЗЈНтЪЭЖрЯюЪНГЫЗЈ![]() ЃЎ
ЃЎ
ФЧУДашгУ2КХПЈЦЌ_________еХЃЌ3КХПЈЦЌ_____________еХ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫљЪіЭМаЮжа,МШЪЧжааФЖдГЦЭМаЮ,гжЪЧжсЖдГЦЭМаЮЕФЪЧ( )
A.ГЄЗНаЮ
B.ЦНааЫФБпаЮ
C.е§ЮхБпаЮ
D.ЕШБпШ§НЧаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіЕШбќШ§НЧаЮЕФБпГЄЗжБ№ЪЧ4cmКЭ7cmЃЌдђЫќЕФжмГЄЪЧ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ2ЃЌНЋГЄЮЊ2ЕФЯпЖЮQFЕФСНЖЫЗХдке§ЗНаЮЯрСкЕФСНБпЩЯЭЌЪБЛЌЖЏЃЎШчЙћЕуQДгЕуAГіЗЂЃЌбиЭМжаЫљЪОЗНЯђАДAЁњBЁњCЁњDЁњAЛЌЖЏЕНЕуAЮЊжЙЃЌЭЌЪБЕуFДгЕуBГіЗЂЃЌбиЭМжаЫљЪОЗНЯђАДBЁњCЁњDЁњAЁњBЛЌЖЏЕНЕуBЮЊжЙЃЌФЧУДдкетИіЙ§ГЬжаЃЌЯпЖЮQFЕФжаЕуMЫљОЙ§ЕФТЗЯпЮЇГЩЕФЭМаЮЕФУцЛ§ЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌAB=ACЃЌЕуDЪЧBCЕФжаЕуЃЌЕуEдкADЩЯЃЎ
ЃЈ1ЃЉЧѓжЄЃКBE=CEЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєBEЕФбгГЄЯпНЛACгкЕуFЃЌЧвBFЁЭACЃЌДЙзуЮЊFЃЌЁЯBAC=45ЁуЃЌдЬтЩшЦфЫќЬѕМўВЛБфЃЎЧѓжЄЃКЁїAEFЁеЁїBCFЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП НЋЕуMЃЈ-5ЃЌyЃЉЯђЩЯЦНвЦ6ИіЕЅЮЛГЄЖШКѓЕУЕНЕФЕугыЕуMЙигкxжсЖдГЦЃЌдђyЕФжЕЪЧЃЈЁЁЁЁЃЉ
A.-6B.6C.-3D.3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтОгУёгУЕчЧщПі,аЁГТдкаЁЧјФкЫцЛњГщВщСЫ30ЛЇМвЭЅЕФдТгУЕчСП,НсЙћШчЯТБэ:
дТгУЕчСП/ЖШ | 40 | 50 | 60 | 80 | 90 | 100 |
ЛЇЪ§ | 6 | 7 | 9 | 5 | 2 | 1 |
дђет30ЛЇМвЭЅЕФдТгУЕчСПЕФжкЪ§КЭжаЮЛЪ§ЗжБ№ЪЧ ( )
A. 60ЃЌ60 B. 60ЃЌ50 C. 50ЃЌ60 D. 50ЃЌ70
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЃЈx+3ЃЉЃЈx+nЃЉ=x2+mxЉ21ЃЌдђmЕФжЕЮЊЃЈЁЁЁЁЃЉ
A.2
B.-2
C.4
D.-4
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com