
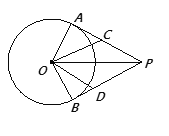
【题目】已知:如图,PA、PB是⊙O的切线;A、B是切点;连结OA、OB、OP.
①若∠COP=∠DOP,求证:AC=BD;
②连结CD,设△PCD的周长为l,若l=2AP,判断直线CD与⊙O的位置关系,并说明理由.
【答案】①详见解析;②直线CD与⊙O相切,理由详见解析.
【解析】
①由(1)知△PAO≌△PBO,得到∠POB=∠POA;再利用AAS判定△AOC≌△BOD,从而得到AC=BD;
②本题要充分利用l=2AP的条件.延长射线PA到F,使AF=BD;易证得△OAF≌△OBD(SAS),得OF=OD;由于l=2AP,即l=PA+PB=PC+PD+CD,因此CD=AC+BD=AC+AF=CF;
在△OCF和△OCD中,OF=OD,OC=OC,FC=CD;可证得△OCF≌△OCD,那么两三角形的对应边上的高也相等,则过O作OE⊥CD,则OE=OA,由此可证得CD与⊙O相切.
①∵∠COP=∠DOP,∠CPO=∠DPO,PO=PO, ∴△OCP≌△ODP,∴CP=DP.
又可证△OPA≌OPB得PA=PB, ∴AC=BD.
②作OE⊥CD于E,设OE=d,CE=x,DE=y. 则d2=AC2+AO2-x2=BD2+OA2-y2.
∴(AC+x)(AC-x)- (BD+y)(BD-y)=0, ∵l=2AP=2BP,∴x+y=AC+BD, ∴AC-x=y-BD.
∴(AC+x)(y-BD)- (BD+y)(BD-y)=0, ∴(y-BD) (AC+x+BD+y)=0.
∵AC+x+BD+y≠0,∴y=BD, 即d=AO,∴直线CD与⊙O相切.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
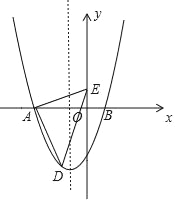
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx﹣3交x轴于点A(﹣3,0)、B(1,0),在y轴上有一点E(0,1),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴下方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣![]() .
.
其中正确结论的个数是( )

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
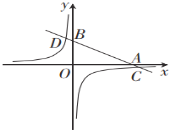
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象分别交x轴、y轴于A、B两点,与反比例函数
的图象分别交x轴、y轴于A、B两点,与反比例函数![]() 的图象交于C、D两点.已知点C的坐标是(6,-1),D(n,3).
的图象交于C、D两点.已知点C的坐标是(6,-1),D(n,3).
(1)求m的值和点D的坐标.
(2)求![]() 的值.
的值.
(3)根据图象直接写出:当x为何值时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
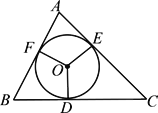
【题目】如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9 cm,BC=14 cm,CA=13 cm,则AF的长为 __________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4,5两月平均每月降价的百分率约是多少?(参考数据:![]() ≈0.95)
≈0.95)
(2)如果房价继续跌落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
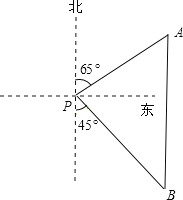
【题目】如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
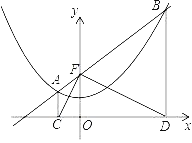
【题目】如图,动直线 y=kx+2(k>0)与 y 轴交于点 F,与抛物线 y=![]() 相交于A,B 两点,过点 A,B 分别作 x 轴的垂线,垂足分别为点 C,D,连接 CF,DF,请你判断△CDF 的形状,并说明理由.
相交于A,B 两点,过点 A,B 分别作 x 轴的垂线,垂足分别为点 C,D,连接 CF,DF,请你判断△CDF 的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字1,2,3;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,﹣3,现从甲袋中随机摸出一个小球,将标有的数字记录为x,再从乙袋中随机摸出一个小球,将标有的数字记录为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com