
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣![]() .
.
其中正确结论的个数是( )

A.4 B.3 C.2 D.1
【答案】B
【解析】
试题分析:由抛物线开口方向得a<0,由抛物线的对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,则可对①进行判断;根据抛物线与x轴的交点个数得到b2﹣4ac>0,加上a<0,则可对②进行判断;利用OA=OC可得到A(﹣c,0),再把A(﹣c,0)代入y=ax2+bx+c得ac2﹣bc+c=0,两边除以c则可对③进行判断;设A(x1,0),B(x2,0),则OA=﹣x1,OB=x2,根据抛物线与x轴的交点问题得到x1和x2是方程ax2+bx+c=0(a≠0)的两根,利用根与系数的关系得到x1x2=![]() ,于是OAOB=﹣
,于是OAOB=﹣![]() ,则可对④进行判断.
,则可对④进行判断.
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,
而a<0,
∴![]() <0,所以②错误;
<0,所以②错误;
∵C(0,c),OA=OC,
∴A(﹣c,0),
把A(﹣c,0)代入y=ax2+bx+c得ac2﹣bc+c=0,
∴ac﹣b+1=0,所以③正确;
设A(x1,0),B(x2,0),
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,
∴x1和x2是方程ax2+bx+c=0(a≠0)的两根,
∴x1x2=![]() ,
,
∴OAOB=﹣![]() ,所以④正确.
,所以④正确.
故选:B.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有何位置关系?(1) r=2cm;(2) r=2.4cm;(3) r=3cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
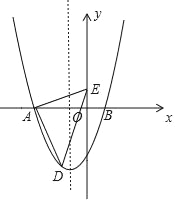
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx﹣3交x轴于点A(﹣3,0)、B(1,0),在y轴上有一点E(0,1),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴下方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
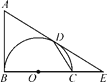
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在D处测得山顶C的仰角为37°,向前走100米来到山脚A处,测得山坡AC的坡度为i=1:0.5,求山的高度(不计测角仪的高度,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
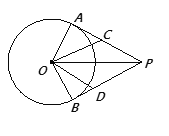
【题目】已知:如图,PA、PB是⊙O的切线;A、B是切点;连结OA、OB、OP.
①若∠COP=∠DOP,求证:AC=BD;
②连结CD,设△PCD的周长为l,若l=2AP,判断直线CD与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
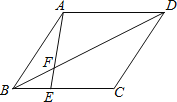
【题目】如图,在ABCD中,E是BC边上一点.且BE=![]() EC,BD,AE相交于点F.
EC,BD,AE相交于点F.
(1)求△BEF的周长与△AFD的周长之比;
(2)若△BEF的面积S△BEF=6cm2.求△AFD的面积S△AFD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com