
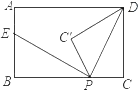
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. 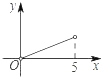 B.
B. 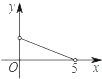 C.
C. 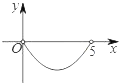 D.
D. 
【答案】D
【解析】
连接DE,根据折叠的性质可得∠CPD=∠C′PD,再根据角平分线的定义可得∠BPE=∠C′PE,然后证明∠DPE=90°,从而得到△DPE是直角三角形,再分别表示出AE、CP的长度,然后利用勾股定理进行列式整理即可得到y与x的函数关系式,根据函数所对应的图象即可得解.
如图,连接DE,
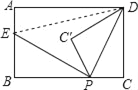
∵△PC′D是△PCD沿PD折叠得到,
∴∠CPD=∠C′PD,
∵PE平分∠BPC′,
∴∠BPE=∠C′PE,
∴∠EPC′+∠DPC′=![]() ×180°=90°,
×180°=90°,
∴△DPE是直角三角形,
∵BP=x,BE=y,AB=3,BC=5,
∴AE=AB﹣BE=3﹣y,CP=BC﹣BP=5﹣x,
在Rt△BEP中,PE2=BP2+BE2=x2+y2,
在Rt△ADE中,DE2=AE2+AD2=(3﹣y)2+52,
在Rt△PCD中,PD2=PC2+CD2=(5﹣x)2+32,
在Rt△PDE中,DE2=PE2+PD2,
则(3﹣y)2+52=x2+y2+(5﹣x)2+32,
整理得,﹣6y=2x2﹣10x,
所以y=﹣![]() x2+
x2+![]() x(0<x<5),
x(0<x<5),
纵观各选项,只有D选项符合.
故选D.


科目:初中数学 来源: 题型:
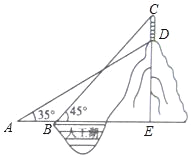
【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的是![]()
![]()
A. “打开电视机,正在播NBA篮球赛”是必然事件
B. “掷一枚硬币正面朝上的概率是![]() ”表示毎抛掷硬币2次就必有1次反面朝上
”表示毎抛掷硬币2次就必有1次反面朝上
C. 一组数据2,3,4,5,5,6的众数和中位数都是5
D. 甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
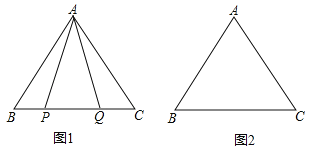
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
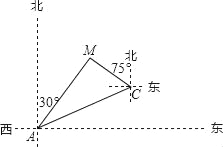
【题目】如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达C处,测得小区M位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,并求AN的长.(精确到1米,![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由![]() 两工程队先后接力完成.
两工程队先后接力完成.![]() 工作队每天整治12米,
工作队每天整治12米,![]() 工程队每天整治8米,共用时20天.
工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
![]()
![]()
![]()
![]() 甲:
甲: ![]() 乙:
乙:
根据甲、乙两名同学所列的方程组,请你分别指出未知数![]() 表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:![]() 表示________________,
表示________________,![]() 表示_______________;
表示_______________;
乙:![]() 表示________________,
表示________________,![]() 表示_______________.
表示_______________.
(2)求![]() 两工程队分别整治河道多少米.(写出完整的解答过程)
两工程队分别整治河道多少米.(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知二次函数![]() 的图象过点
的图象过点![]() .
.
![]() 若
若![]() ,求函数的表达式;
,求函数的表达式;
![]() 若函数图象的顶点在x轴上,求a的值;
若函数图象的顶点在x轴上,求a的值;
![]() 已知点
已知点![]() 和
和![]() 都在该函数图象上,试比较m、n的大小.
都在该函数图象上,试比较m、n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() .
.
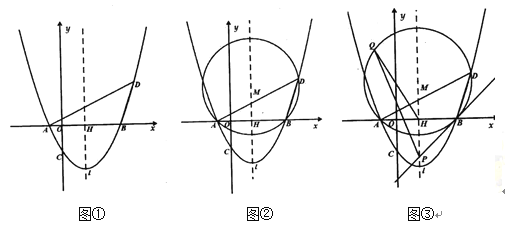
(1)求过点![]() 、
、![]() 、
、![]() 三点的抛物线解析式;
三点的抛物线解析式;
(2)在抛物线上取点![]() ,若点
,若点![]() 的横坐标为10,求点
的横坐标为10,求点![]() 的坐标及
的坐标及![]() 的度数;
的度数;
(3)设抛物线对称轴![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 的外接圆圆心为
的外接圆圆心为![]() (如图②)
(如图②)
①求点![]() 的坐标及⊙
的坐标及⊙![]() 的半径;
的半径;
②过点![]() 作⊙
作⊙![]() 的切线交于
的切线交于![]() 于点
于点![]() (如图③),设
(如图③),设![]() 为⊙
为⊙![]() 上一动点,则在点
上一动点,则在点![]() 运动过程中
运动过程中![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com