
【题目】已知直线![]() 平行
平行![]() ,直线
,直线![]() 分别截
分别截![]() 、
、![]() 于点
于点![]() 、
、![]() 两点.
两点.
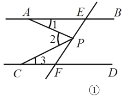
(1)如图①,有一动点![]() 在线段
在线段![]() 之间运动(不与E,F两点重合),试探究
之间运动(不与E,F两点重合),试探究![]() 、
、![]() 、
、![]() 的等量等关系?试说明理由.
的等量等关系?试说明理由.
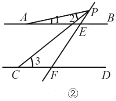
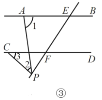
(2)如图②、③,当动点![]() 在线段
在线段![]() 之外运动(不与E,F两点重合),问上述结论是否还成立?若不成立,试写出新的结论并说明理由.
之外运动(不与E,F两点重合),问上述结论是否还成立?若不成立,试写出新的结论并说明理由.
【答案】(1)∠2=∠1+∠3,理由见解析;(2)∠2=∠1+∠3不成立,新的结论为∠2=![]() ,理由见解析.
,理由见解析.
【解析】
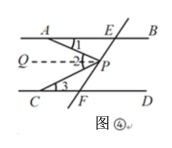
(1)如图④,过点 P作PQ∥AB,则∠1=∠APQ,根据平行线的性质,即可得到结论;
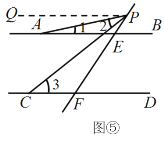
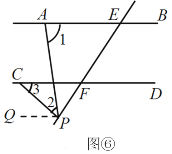
(2)分两种情况:(i)当点P在FE的延长线上时,如图⑤,过点 P作PQ∥AB,(ii)当点P在EF的延长线上时,如图⑥,过点 P作PQ∥AB,分别求出∠2、∠1、∠3的数量关系,即可得到结论.
(1)∠2=∠1+∠3,理由如下:
如图④,过点 P作PQ∥AB,则∠1=∠APQ.
∵AB∥CD,PQ∥AB,
∴PQ∥CD,
∴∠3=∠CPQ.
∵∠2=∠APQ+∠CPQ=∠1+∠3;
(2)∠2=∠1+∠3 不成立,新的结论为∠2=![]() .理由如下:
.理由如下:
(i)当点P在FE的延长线上时,
如图⑤,过点 P作PQ∥AB,则∠1=∠APQ.
∵AB∥CD,PQ∥AB,
∴PQ∥CD,
∴∠3=∠CPQ.
∴∠2=∠CPQ![]() ∠APQ=∠3
∠APQ=∠3![]() ∠1;
∠1;
(ii)当点P在EF的延长线上时,
如图⑥,过点 P作PQ∥AB,则∠1=∠APQ.
∵AB∥CD,PQ∥AB,
∴PQ∥CD,
∴∠3=∠CPQ,
∴∠2=∠APQ![]() ∠CPQ=∠1
∠CPQ=∠1![]() ∠3.
∠3.
综上所述:∠2=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.
求证:(1)△ABC≌△DEF;
(2)如果∠ACB=25°,求∠AGF的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电超市经营甲、乙两种品牌的洗衣机.经投标发现,1台甲品牌冼衣机进价比1台乙品牌洗衣机进价贵500元;购进2台甲品牌洗衣机和3台乙品牌洗衣机共需进货款13500元.
(1)购进1台甲品牌洗衣机和1台乙品牌洗衣机进价各需要多少元?
(2)超市根据经营实际情况,需购进甲、乙两种品牌的洗衣机总数为50台,购进甲、乙两种品牌的洗衣机的总费用不超过145250元.
①请问甲品牌洗衣机最多购进多少台?
②超市从经营实际需要出发,其中甲品牌洗衣机购进的台数不少于乙晶牌冼衣机台数的3倍,则该超市共有几种购进方案?试写出所有的购进方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
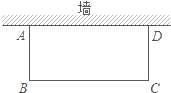
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有400名学生,为了解该年级学生上学的交通方式,从中随机抽取100名学生进行问卷调查,并对调查数据进行整理、描述和分析,下面给出了部分信息
A.不同交通方式学生人数分布统计图如下:

B.采用公共交通方式单程所花费时间(分钟)的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);

根据以上信息,完成下列问题:
(1)补全频数分布直方图;
(2)根据不同交通方式学生人数所占的百分比,算出“私家车方式”对应扇形的圆心角是度_____.
(3)请你估计全年级乘坐公共交通上学有_____人,其中单程不少于60分钟的有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=9,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).

(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com