
 白日登山望烽火,黄昏饮马傍交河.诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A点出发,奔向小河旁边的P点饮马,饮马后再到B点宿营,若A、B到水平直线L(L表示小河)的距离分别是2,1,AB两点之间水平距离是4,则AP+PB最小值=5.
白日登山望烽火,黄昏饮马傍交河.诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A点出发,奔向小河旁边的P点饮马,饮马后再到B点宿营,若A、B到水平直线L(L表示小河)的距离分别是2,1,AB两点之间水平距离是4,则AP+PB最小值=5. 分析 首先作A关于直线l的对称点A′,连接A′B交直线l于点P,此时AP+PB最小;然后可得AP+PB的最小值=A′B,再利用勾股定理求解,即可求得答案.
解答 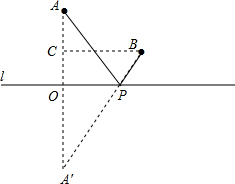 解:作A关于直线l的对称点A′,连接A′B交直线l于点P,此时AP+PB最小;
解:作A关于直线l的对称点A′,连接A′B交直线l于点P,此时AP+PB最小;
则PA=PA′,
∴AP+PB=PA′+PA=A′B,
过点B作BC⊥AA′于点C,
则OA′=OA=2,OC=1,BC=4,
∴A′C=OA′+OC=2+1=3,
∴A′B=$\sqrt{A′{C}^{2}+B{C}^{2}}$=5.
∴AP+PB最小值=5.
故答案为:5.
点评 此题考查了最短路径问题以及勾股定理.注意准确找到点P的位置是解此题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=$\frac{-1}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=$\frac{-4}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
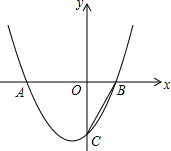 如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.
如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
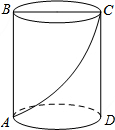 如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,求昆虫爬行的最短路程.
如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,求昆虫爬行的最短路程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com