
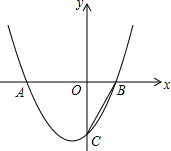
 如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.
如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.分析 (1)先利用勾股定理计算出OC=2得到C点坐标,然后把B、C两点坐标代入y=x2+bx+c中求出b、c,然后利用二次函数的性质求函数的最小值;
(2)设OB=t,则OC=2t,则B(t,0),C(0,-2t),把它们代入y=x2+bx+c得$\left\{\begin{array}{l}{{t}^{2}+tb+c=0}\\{c=-2t}\end{array}\right.$,解关于b、c的方程组得$\left\{\begin{array}{l}{b=2-t}\\{c=-2t}\end{array}\right.$,则抛物线解析式为y=x2+(2-t)x-2t,设顶点的坐标为(m,n),利用抛物线顶点坐标公式得到m=-$\frac{2-t}{2}$,n=-$\frac{(t+2)^{2}}{4}$,然后消去t得到m与n的关系式即可.
解答 解:(1)∵x2=1,即B(1,0),
∴OB=1,
∴OC=$\sqrt{B{C}^{2}-O{B}^{2}}$=$\sqrt{(\sqrt{5})^{2}-{1}^{2}}$=2,
∴C(0,-2),
把B(1,0),C(0,-2)代入y=x2+bx+c得$\left\{\begin{array}{l}{1+b+c=0}\\{c=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=1}\\{c=-2}\end{array}\right.$,
∴抛物线解析式为y=x2+x-2,
∴函数y=x2+bx+c的最小值=$\frac{4×1×(-2)-{1}^{2}}{4×1}$=-$\frac{9}{4}$;
(2)设OB=t,则OC=2t,
∴B(t,0),C(0,-2t),
把B(t,0),C(0,-2t)代入y=x2+bx+c得$\left\{\begin{array}{l}{{t}^{2}+tb+c=0}\\{c=-2t}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=2-t}\\{c=-2t}\end{array}\right.$,
∴抛物线解析式为y=x2+(2-t)x-2t,
设顶点的坐标为(m,n),
则m=-$\frac{2-t}{2}$,n=$\frac{4×1×(-2t)-(2-t)^{2}}{4}$=-$\frac{{t}^{2}+4t+4}{4}$=-$\frac{(t+2)^{2}}{4}$,
把t=2m+2代入得n=-$\frac{(2m+4)^{2}}{4}$=-m2-4m-4(-1<m<0).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题化为解关于x的一元二次方程.本题的关键是记住抛物线的顶点坐标公式.


科目:初中数学 来源: 题型:选择题
| 班级 | 参加人数 | 中位数 | 平均数 | 方差 |
| 一 | 49 | 84 | 80 | 186 |
| 二 | 49 | 85 | 80 | 161 |
| A. | ①② | B. | ①③ | C. | ①②③ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 白日登山望烽火,黄昏饮马傍交河.诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A点出发,奔向小河旁边的P点饮马,饮马后再到B点宿营,若A、B到水平直线L(L表示小河)的距离分别是2,1,AB两点之间水平距离是4,则AP+PB最小值=5.
白日登山望烽火,黄昏饮马傍交河.诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A点出发,奔向小河旁边的P点饮马,饮马后再到B点宿营,若A、B到水平直线L(L表示小河)的距离分别是2,1,AB两点之间水平距离是4,则AP+PB最小值=5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
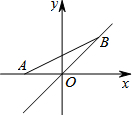 如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com