
分析 (1)先根据绝对值的意义化简绝对值,再算乘方后计算乘除最后算加减,有括号的先算括号里面的;
(2)按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的;
(3)和(4)运用整式的加减运算顺序,先去括号,再合并同类项.
解答 解(1)-52×|1-$\frac{19}{15}$|$+\frac{3}{4}$×[(-$\frac{4}{3}$)2-23]
=-25×$\frac{4}{15}$$+\frac{3}{4}$×[$\frac{16}{9}$-8]
=-$\frac{20}{3}$$+\frac{3}{4}$×[-$\frac{56}{9}$]
=-$\frac{20}{3}$-$\frac{14}{3}$
=-$\frac{34}{3}$;
(2)-23÷(-$\frac{1}{8}$)-$\frac{1}{4}$×(-2)2+(-2)÷(-$\frac{2}{5}$)×$\frac{1}{5}$
=-8×(-8)-$\frac{1}{4}$×4+(-2)×(-$\frac{5}{2}$)×$\frac{1}{5}$
=64-1+1
=64;
(3)2a2-[$\frac{1}{2}$(ab-a2)+8ab]$-\frac{1}{2}ab$
=2a2-[$\frac{1}{2}$ab-$\frac{1}{2}$a2+8ab]$-\frac{1}{2}ab$
=2a2-$\frac{1}{2}$ab+$\frac{1}{2}$a2-8ab$-\frac{1}{2}ab$
=$\frac{5}{2}$a2-9ab;
(4)4x2y-[6xy-3(4xy-2)-x2y]+1
=4x2y-[6xy-12xy+6-x2y]+1
=4x2y-6xy+12xy-6+x2y+1
=5x2y+6xy-5.
点评 本题考查的是有理数的运算能力.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.
(3)整式中如果有多重括号应按照先去小括号,再去中括号,最后大括号的顺序进行.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
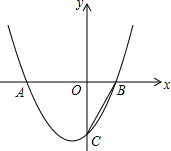 如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.
如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com