
【题目】感知定义
在一次数学活动课中,老师给出这样一个新定义:如果三角形的两个内角α与β满足α+2β=90°,那么我们称这样的三角形为“类直角三角形”.
尝试运用
(1)如图1,在Rt△ABC中,∠C=90°,BC=3,AB=5,BD是∠ABC的平分线.
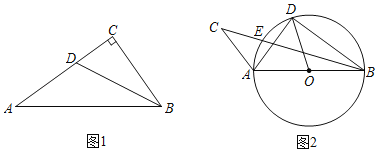
①证明△ABD是“类直角三角形”;
②试问在边AC上是否存在点E(异于点D),使得△ABE也是“类直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
类比拓展
(2)如图2,△ABD内接于⊙O,直径AB=10,弦AD=6,点E是弧AD上一动点(包括端点A,D),延长BE至点C,连结AC,且∠CAD=∠AOD,当△ABC是“类直角三角形”时,求AC的长.
【答案】(1)①证明见解析;②CE=![]() ;(2)当△ABC是“类直角三角形”时,AC的长为
;(2)当△ABC是“类直角三角形”时,AC的长为![]() 或
或![]() .
.
【解析】
(1)①证明∠A+2∠ABD=90°即可解决问题.
②如图1中,假设在AC边设上存在点E(异于点D),使得△ABE是“类直角三角形”,证明△ABC∽△BEC,可得![]() ,由此构建方程即可解决问题.
,由此构建方程即可解决问题.
(2)分两种情形:①如图2中,当∠ABC+2∠C=90°时,作点D关于直线AB的对称点F,连接FA,FB.则点F在⊙O上,且∠DBF=∠DOA.
②如图3中,由①可知,点C,A,F共线,当点E与D共线时,由对称性可知,BA平分∠FBC,可证∠C+2∠ABC=90°,利用相似三角形的性质构建方程即可解决问题.
(1)①证明:如图1中,
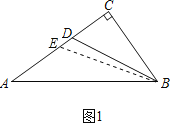
∵BD是∠ABC的角平分线,
∴∠ABC=2∠ABD,
∵∠C=90°,
∴∠A+∠ABC=90°,
∴∠A+2∠ABD=90°,
∴△ABD为“类直角三角形”;
②如图1中,假设在AC边设上存在点E(异于点D),使得△ABE是“类直角三角形”,
在Rt△ABC中,∵AB=5,BC=3,
∴AC=![]() ,
,
∵∠AEB=∠C+∠EBC>90°,
∴∠ABE+2∠A=90°,
∵∠ABE+∠A+∠CBE=90°,
∴∠A=∠CBE,
∴△ABC∽△BEC,
∴![]() ,
,
∴CE=![]() ,
,
(2)∵AB是直径,
∴∠ADB=90°,
∵AD=6,AB=10,
∴BD=![]() ,
,
①如图2中,当∠ABC+2∠C=90°时,作点D关于直线AB的对称点F,连接FA,FB,则点F在⊙O上,且∠DBF=∠DOA,
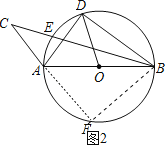
∵∠DBF+∠DAF=180°,且∠CAD=∠AOD,
∴∠CAD+∠DAF=180°,
∴C,A,F共线,
∵∠C+∠ABC+∠ABF=90°,
∴∠C=∠ABF,
∴△FAB∽△FBC,
∴![]() ,即
,即![]() ,
,
∴AC=![]() .
.
②如图3中,由①可知,点C,A,F共线,当点E与D共线时,由对称性可知,BA平分∠FBC,
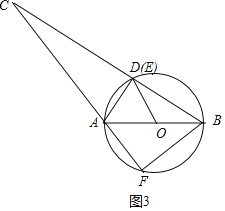
∴∠C+2∠ABC=90°,
∵∠CAD=∠CBF,∠C=∠C,
∴△DAC∽△FBC,
∴![]() ,即
,即![]() ,
,
∴CD=![]() (AC+6),
(AC+6),
在Rt△ADC中,[ ![]() (ac+6)]2+62=AC2,
(ac+6)]2+62=AC2,
∴AC=![]() 或﹣6(舍弃),
或﹣6(舍弃),
综上所述,当△ABC是“类直角三角形”时,AC的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,是住宅区内的两幢楼,它们的高![]() ,两楼间的距离
,两楼间的距离![]() ,现需了解甲楼对乙楼的采光的影响情况.
,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为![]() 角时,求甲楼的影子在乙楼上有多高(答案可用根号表示);
角时,求甲楼的影子在乙楼上有多高(答案可用根号表示);
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着网购的日益盛行,物流行业已逐渐成为运输业的主力,已知某大型物流公司有A、B两种型号的货车,A型货车的满载量是B型货车满载量的2倍多4吨,在两车满载的情况下,用A型货车载1400吨货物与用B型货车载560吨货物的用车数量相同.
(1)1辆A型货车和1辆B型货车的满载量分别是多少?
(2)该物流公司现有120吨货物,可以选择上述两种货车运送,在满载的情况下,有几种方案可以一次性运完?
查看答案和解析>>
科目:初中数学 来源: 题型:
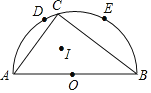
【题目】如图,已知点D,E是半圆O上的三等分点,C是弧DE上的一个动点,连结AC和BC,点I是△ABC的内心,若⊙O的半径为3,当点C从点D运动到点E时,点I随之运动形成的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
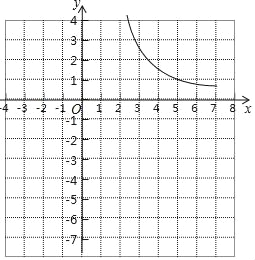
【题目】小邱同学根据学习函数的经验,研究函数y=![]() 的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
x | 1 |
|
|
| 3 | 4 | 5 | 6 | … |
y | ﹣1 | ﹣2 | ﹣3.4 | ﹣7.5 | 2.4 | 1.4 | 1 | 0.8 | … |
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)在图中补全当1≤x<2的函数图象;
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() =x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:

(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
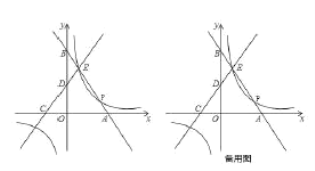
【题目】如图,平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,直线
,直线![]() 与
与![]() 相交于点
相交于点![]() ,线段
,线段![]() 、
、![]() 的长是-元二次方程
的长是-元二次方程![]() 的两根(
的两根(![]() ),
), ![]() ,点
,点![]() 的横坐标为3,反比例函数
的横坐标为3,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)若直线![]() 与反比例函数图象上除点
与反比例函数图象上除点![]() 外的另一交点为
外的另一交点为![]() ,求
,求![]() 的面积:若点
的面积:若点![]() 在
在![]() 轴上,若点
轴上,若点![]() 在
在![]() 轴上,求
轴上,求![]() 的最小值:
的最小值:
(2)若点![]() 在坐标轴.上,在平面内存在一点
在坐标轴.上,在平面内存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形且线段
为顶点的四边形是矩形且线段![]() 为矩形的一条边, 直接写出符合条件的
为矩形的一条边, 直接写出符合条件的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
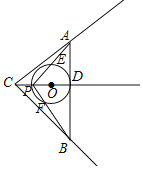
【题目】如图,在△ABC中,AB=7,BC=4![]() ,∠ABC=45°,射线CD⊥AB于D,点P为射线CD上一动点,以PD为直径的⊙O交PA、PB分别为E、F,设CP=x.
,∠ABC=45°,射线CD⊥AB于D,点P为射线CD上一动点,以PD为直径的⊙O交PA、PB分别为E、F,设CP=x.
(1)求sin∠ACD的值.
(2)在点P的整个运动过程中:
①当⊙O与射线CA相切时,求出所有满足条件时x的值;
②当x为何值时,四边形DEPF为矩形,并求出矩形DEPF的面积.
(3)如果将△ADC绕点D顺时针旋转150°,得△A′DC′,若点A′和点C′有且只有一个点在圆内,则x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com