【题目】如图所示，能说明四边形
是菱形的有（ ）
①
；②
，
，
；③
；④
，．
A. ① B. ①③ C. ② D. ③④
【答案】C
【解析】
选项A，不能说明四边形
是菱形，条件①只能说明四边形ABCD的对角线互相垂直；
选项B，不能说明四边形是菱形，条件①③只说明四边形ABCD的对角线相等且互相垂直；
选项C，由OA=OC，OB=OD能证出为平行四边形，再由AB=BC，根据一组邻边相等的平行四边形是菱形即可证得四边形ABCD是菱形；
选项D，不能说明四边形是菱形，条件④能证出四边形ABCD是平行四边形，再由条件③即可证得四边形ABCD为矩形．
故选C．
本题考查菱形的判定方法. 菱形的判定方法有三种：①定义：一组邻边相等的平行四边形是菱形；②四条边相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形．
科目：初中数学 来源： 题型：
【题目】将矩形纸片分别沿两条不同的直线剪两刀，可以使剪得的三块纸片恰能拼成一个等腰三角形（不能有重叠和缝隙）．小华的做法是：如图1所示，在矩形ABCD中，分别取AD、AB、CD的中点P、E、F，并沿直线PE 、PF剪两刀，所得的三部分可拼成等腰三角形△PMN (如图2)．
（1）在图3中画出另一种剪拼成等腰三角形的示意图；
（2）以矩形ABCD的顶点B为原点，BC所在直线为x轴建立平面直角坐标系（如图4），矩形ABCD剪拼后得到等腰三角形△PMN，点P在边AD上（不与点A、D重合），点M、N在x轴上（点M在N的左边）．如果点D的坐标为(5，8)，直线PM的解析式为y=kx+b，求所有满足条件的k的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰三角形ABC的底边BC长为6，面积是36，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为______．
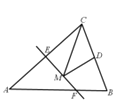
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，已知点A(-1，4)，B(-2，2)，C(1，1).
(1)作ΔABC关于x轴对称的△A1B1C1，并写出点A1，B1，C1的坐标，
(2)作△ABC关于y轴对称的△A2B2C2，并写出点A2，B2，C2的坐标，
(3)观察点A1，B1，C1和A2，B2，C2的坐标，请用文字语言归纳点A1和A2，B1和B2，C1和C2坐标之间的关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)如图1，将两个全等的三角板如图摆放，其中△ABC和ΔADE的直角顶点重合在点A处，∠ADE=∠ABC=60°，且点D在AC上，点B在AE上，∠C=∠E=30°，AB=AD，AC=AE，BC=DE，BC和DE相交于点F.求证:CF=EF.
(2)如图2，将这两个三角板如图摆放，直角顶点A仍然重合，BC与DE相交于点F，AC与DE交于点M，AE和BC交于点N.猜想CF和EF还相等吗?说明理由.
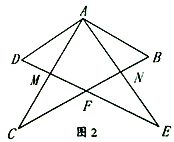
(3)如图3，在(2)的基础上，若∠DAM=30°.求证:线段DF和AC互相垂直平分.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请阅读下列材料：
问题：如图，在正方形
和平行四边形
中，点
，
，
在同一条直线上，
是线段
的中点，连接
，
．
探究：当与的夹角为多少度时，平行四边形是正方形？
小聪同学的思路是：首先可以说明四边形是矩形；然后延长
交
于点
，构造全等三角形，经过推理可以探索出问题的答案．
请你参考小聪同学的思路，探究并解决这个问题．
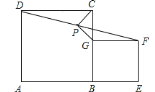
（1）求证：四边形是矩形；
（2）与的夹角为________度时，四边形是正方形．
理由：
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
