Question

14．如图，在△ABC中，∠BAC=90°，AB=AC，∠ABD=∠BAD=15°，求证：AC=DC．

Answer 1

分析 首先构造△ACD′，D′在△ABC内部，使得AD′=CD′，∠D′AC=∠D′CA=15°，连DD′，证明△ABD≌△ACD′，得到AD=AD′，进一步证明△ADD′是等边三角形，得到DD′=AD′，再证明△ACD'≌△DCD'，即可得到AC=DC．

解答 解：如图，构造△ACD′，D′在△ABC内部，使得AD′=CD′，∠D′AC=∠D′CA=15°，连DD′，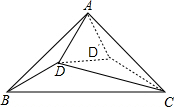

∵∠ABD=∠BAD=15°，
∴∠ABD=∠BAD=∠D′AC=∠D′CA，
在△ABD和△ACD′中，
$\left\{\begin{array}{l}{∠D′AC=∠BAD}\\{AB=AC}\\{∠ACD′=∠ABD}\end{array}\right.$，
∴△ABD≌△ACD′，
∴AD=AD′，
∵∠DAD′=∠BAC-∠BAD′-∠CAD=90°-15°-15°=60°，
∴△ADD′是等边三角形，
∴DD′=AD′，
∵∠CD′A=180-∠CAD′-∠ACD′=180°-15°-15°=150°，
∴∠CDD′=360°-∠CD′A-∠AD′D=360°-150°-60°=150°，
∴∠CD′A=∠CDD′，
在△ACD′和△DCD′中，
$\left\{\begin{array}{l}{AD′=DD′}\\{∠AD′C=∠DD′C}\\{CD′=CD′}\end{array}\right.$，
∴△ACD'≌△DCD'
∴AC=DC．

点评 本题考查了全等三角形的性质定理与判定定理，解决本题的关键是构建全等三角形．