练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一个半径为r的圆形纸片在边长为a（ ）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）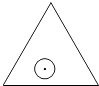
    A.
    B.
    C.
    D.πr2

    【答案】C
    【解析】如图，当圆形纸片运动到与A的两边相切的位置时，

    过圆形纸片的圆心O1作两边的垂线，垂足分别为D，E，
    连接AO1，则RtADO1中，O1AD=30，O1D=r，AD=r，
    ∴SADO1=O1DAD=r2，由此S四边形ADO1E=2SADO1=r2，
    ∵由题意，DO1E=120，得S扇形O1DE=r2，
    ∴圆形纸片“不能接触到的部分”的面积是3（r2-r2）=（）r2 .
    所以答案是：C.
    【考点精析】认真审题，首先需要了解切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．
    （1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；
    （2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种动物的身高y（dm）是其腿长x（dm）的一次函数．当动物的腿长为6dm时，身高为45.5dm；当动物的腿长为14dm时，身高为105.5dm．

    （1）写出y与x之间的关系式；

    （2）当该动物腿长10dm时，其身高为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，点C在AOB的一边OA上，过点C的直线DE//OB，CF平分ACD，CG CF于C ．

    （1）若O =40，求ECF的度数；

    （2）求证：CG平分OCD；

    （3）当O为多少度时，CD平分OCF，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABC中，D是AB上的一点，且AD＝2BD，E是BC的中点，CD、AE相交于点F．若EFC的面积为1，则ABC的面积为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，图中二次函数解析式为y=ax2+bx+c（a≠0）则下列命题中正确的有（填序号）．①abc＞0；②b2＜4ac；③4a﹣2b+c＞0；④2a+b＞c．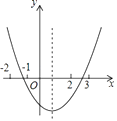

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学习几何的一个重要方法就是要学会抓住基本图形，让我们来做一次研究性学习．

    （1）如图①所示的图形，像我们常见的学习用品一圆规，我们常把这样的图形叫做“规形图”．请你观察“规形图”，试探究∠BOC与∠A、∠B、∠C之间的关系，并说明理由：

    （2）如图②，若△ABC中，BO平分∠ABC，CO平分∠ACB，且它们相交于点O，试探究∠BOC与∠A的关系；

    （3）如图③，若△ABC中，∠ABO=∠ABC，∠ACO=∠ACB，且BO、CO相交于点O，请直接写出∠BOC与∠A的关系式为　　　　_．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线C1：y=x2+bx+c经过原点，与x轴的另一个交点为（2，0），将抛物线C1向右平移m（m＞0）个单位得到抛物线C2 ， C2交x轴于A，B两点（点A在点B的左边），交y轴于点C．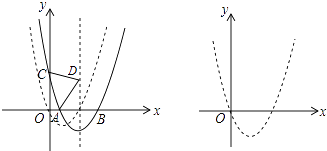
    （1）求抛物线C1的解析式及顶点坐标；
    （2）以AC为斜边向上作等腰直角三角形ACD，当点D落在抛物线C2的对称轴上时，求抛物线C2的解析式；
    （3）若抛物线C2的对称轴存在点P，使△ PAC为等边三角形，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校在疫情期间利用网络组织了一次防“新冠病毒”知识竞赛，评出特等奖10人，优秀奖20人．学校决定给所有获奖学生各发一份奖品，同一等次的奖品相同．

    （1）（列方程组解应用题）若特等奖和优秀奖的奖品分别是口罩和温度计，口罩单价的2倍与温度计单价的3倍相等，购买这两种奖品一共花费700元，求口罩和温度计的单价各是多少元？

    （2）（利用不等式或不等式组解应用题）若两种奖品的单价都是整数，且要求特等奖单价比优秀奖单价多20元．在总费用不少于440而少于500元的前提下，购买这两种奖品时它们的单价有几种情况，请分别求出每种情况特等奖和优秀奖奖品的单价．

    查看答案和解析>>

    同步练习册答案