
【题目】我们把1°的圆心角所对的弧叫做1°的弧.由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,已知,![]() 的度数为
的度数为![]() ,
,![]() 的度数为
的度数为![]() .
.
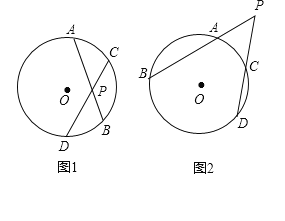
(1)如图1,⊙O的两条弦AB、CD相交于圆内一点P,求证:![]() ;
;
(2)如图2,⊙O的两条弦AB、CD延长线相交于圆外一点P.问题(1)中的结论是否成立?如果成立,给予证明;如果不成立,写出一个类似的结论,并证明.
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤4元的价格购进某种水果若干斤,然后以每斤6元的价格出售,每天可售出150斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出30斤,为保证每天至少售出360斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利450元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )

A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
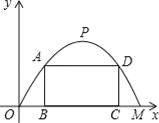
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其顶点为
,其顶点为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() .
.
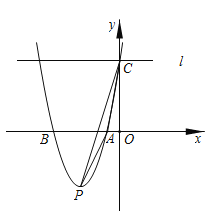
(1)求点![]() 的坐标;
的坐标;
(2)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的3倍?若存在,求出点
的面积的3倍?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于钝角α,定义它的三角函数值如下:
sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α)
(1)求sin120°,cos120°,sin150°的值;
(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司11月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出![]() 部汽车,则该部汽车的进价为
部汽车,则该部汽车的进价为![]() 万元,每多售出
万元,每多售出![]() 部,所有售出的汽车的进价均降低
部,所有售出的汽车的进价均降低![]() 万元/部.月底厂家再根据销售量返利给销售公司:销售量在
万元/部.月底厂家再根据销售量返利给销售公司:销售量在![]() 部以内(含
部以内(含![]() 部),每部返利
部),每部返利![]() 万元;销售量在
万元;销售量在![]() 部以上,每部返利
部以上,每部返利![]() 万元.
万元.
(1)若该公司当月售出![]() 部汽车,则每部汽车的进价为 万元;
部汽车,则每部汽车的进价为 万元;
(2)若汽车的售价为![]() 万元/部,该公司计划当月盈利
万元/部,该公司计划当月盈利![]() 万元,则需售出多少部汽车? (盈利=销售利润+返利)
万元,则需售出多少部汽车? (盈利=销售利润+返利)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com