
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α,
(1)如图1所示,当α=60°时,求证:△DCE是等边三角形;
(2)如图2所示,当α=45°时,求证:![]() =
=![]() ;
;
(3)如图3所示,当α为任意锐角时,请直接写出线段CE与DE的数量关系:![]() =_____.
=_____.



【答案】1
【解析】试题(1)证明△CFD≌△DAE即可解决问题.
(2)如图2中,作FG⊥AC于G.只要证明△CFD∽△DAE,推出![]() =
=![]() ,再证明CF=
,再证明CF=![]() AD即可.
AD即可.
(3)证明EC=ED即可解决问题.
试题解析:(1)证明:如图1中,∵∠ABC=∠ACB=60°,∴△ABC是等边三角形,∴BC=BA.∵DF∥AC,∴∠BFD=∠BCA=60°,∠BDF=∠BAC=60°,∴△BDF是等边三角形,∴BF=BD,∴CF=AD,∠CFD=120°.∵AE∥BC,∴∠B+∠DAE=180°,∴∠DAE=∠CFD=120°.∵∠CDA=∠B+∠BCD=∠CDE+∠ADE.∵∠CDE=∠B=60°,∴∠FCD=∠ADE,∴△CFD≌△DAE,∴DC=DE.∵∠CDE=60°,∴△CDE是等边三角形.

(2)证明:如图2中,作FG⊥AC于G.∵∠B=∠ACB=45°,∴∠BAC=90°,∴△ABC是等腰直角三角形.∵DF∥AC,∴∠BDF=∠BAC=90°,∴∠BFD=45°,∠DFC=135°.∵AE∥BC,∴∠BAE+∠B=180°,∴∠DFC=∠DAE=135°.∵∠CDA=∠B+∠BCD=∠CDE+∠ADE.∵∠CDE=∠B=45°,∴∠FCD=∠ADE,∴△CFD∽△DAE,∴![]() =
=![]() .∵四边形ADFG是矩形,FC=
.∵四边形ADFG是矩形,FC=![]() FG,∴FG=AD,CF=
FG,∴FG=AD,CF=![]() AD,∴
AD,∴![]() =
=![]() .
.

(3)解:如图3中,设AC与DE交于点O.

∵AE∥BC,∴∠EAO=∠ACB.∵∠CDE=∠ACB,∴∠CDO=∠OAE.∵∠COD=∠EOA,∴△COD∽△EOA,∴![]() =
=![]() ,∴
,∴![]() =
=![]() .∵∠COE=∠DOA,∴△COE∽△DOA,∴∠CEO=∠DAO.∵∠CED+∠CDE+∠DCE=180°,∠BAC+∠B+∠ACB=180°.∵∠CDE=∠B=∠ACB,∴∠EDC=∠ECD,∴EC=ED,∴
.∵∠COE=∠DOA,∴△COE∽△DOA,∴∠CEO=∠DAO.∵∠CED+∠CDE+∠DCE=180°,∠BAC+∠B+∠ACB=180°.∵∠CDE=∠B=∠ACB,∴∠EDC=∠ECD,∴EC=ED,∴![]() =1.
=1.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】在生活中,人们经常通过一些标志性建筑确定位置,在数学中往往也是这样.
(1)将正整数如图1的方式进行排列:

小明同学通过仔细观察,发现每一行第一列的数字有一定的规律,所以每一行第一列的数字可以作为标志数,于是他认为第七行第一列的数字是 ,第7行、第5列的数字是 .
(2)方法应用
观察下面一列数:1,﹣2,3,﹣4,5,﹣6,7,…并将这列数按照如图2方式进行排列:
按照上述方式排列下去,
问题1:第10行从左边数第9个数是 ;
问题2:第n行有 个数;(用含n的代数式表示)
问题3:数字2019在第 行,从左边数第 个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB//CD,

(1) 求∠1+∠2+∠3的度数.
(2) ∠1+∠2+∠3+∠4 = .
根据以上的规律求∠1+∠2+∠3+…+∠n = .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年深圳进行高中招生制度改革,某初中学校获得保送(指标生)名额若干,现在九年级四位品学兼优的学生小斌(男)、小亮(男)、小红(女)、小丽(女)都获得保送资格,且机会均等.
(1)若学校只有一个名额,则随机选到小斌的概率是多少.
(2)若学校争取到两个名额,请用树状图或列表法求随机选到保送的学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线交AD、BC于点E、F,AC与EF交于点O,连结AF、CE.
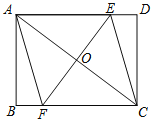
(1)求证:四边形AFCE是菱形;
(2)若AB=3,AD=4,求菱形AFCE的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:甲同学解方程![]() ,如下:
,如下:
甲:![]() 第一步
第一步
![]() 第二步
第二步
![]() 第三步
第三步
![]() 第四步
第四步
![]() 第五步
第五步
(1)他的解法第______步开始出现错误
(2)请把正确的解题过程写在右侧横线上,并在括号内填上对应步骤的理论依据.
正确解法:
去分母:__________________(___________________)
去括号:___________________
移项:__________________________
合并同类项:_______________________________
系数化1:_________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络商店(简称网店)是近年来迅速兴起的一种电子商务形式,小明的网店销售红枣、小米两种商品的相关信息如下表:
商品 | 红枣 | 小米 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 40 | 38 |
售价(元/袋) | 60 | 54 |
根据上表提供的信息,解答下列问题
(1)已知今年前四个月,小明的网店销售上表中规格的红枣和小米共2000kg,获得利润2.8万元,求这前四个月小明的网店销售这种规格的红枣和小米各多少袋?
(2)根据之前的销售情况,估计今年5月到12月这后八个月,小明的网店还能销售同规格的红枣和小米共4000kg,其中,红枣的销售量不低于1200kg.假设这后八个月,销售红枣x(kg),销售红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后八个月,小明的网店销售这种规格的红枣和小米至少获得总利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月4日,中国国际女足锦标赛半决赛在武汉进行,这场由中国队迎战俄罗斯队的比赛牵动着众多足球爱好者的心.在未开始检票入场前,已有1200名足球爱好者排队等待入场.假设检票开始后,每分钟赶来的足球爱好者人数是固定的,1个检票口每分钟可以进入40人.如果4个检票口同时检票,15分钟后排队现象消失;如果7个检票口同时检票,_____分钟后排队现象消失.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com