
在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.


【考点】二次函数综合题;待定系数法求二次函数解析式.
【专题】压轴题.
【分析】(1)先假设出函数解析式,利用三点法求解函数解析式.
(2)设出M点的坐标,利用S=S△AOM+S△OBM﹣S△AOB即可进行解答;
(3)当OB是平行四边形的边时,表示出PQ的长,再根据平行四边形的对边相等列出方程求解即可;当OB是对角线时,由图可知点A与P应该重合.
【解答】解:(1)设此抛物线的函数解析式为:
y=ax2+bx+c(a≠0),
将A(﹣4,0),B(0,﹣4),C(2,0)三点代入函数解析式得:


解得
 ,
,
所以此函数解析式为:y=
 ;
;
(2)∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为:(m,
 ),
),
∴S=S△AOM+S△OBM﹣S△AOB
=
 ×4×(﹣
×4×(﹣
 m2﹣m+4)+
m2﹣m+4)+
 ×4×(﹣m)﹣
×4×(﹣m)﹣
 ×4×4
×4×4
=﹣m2﹣2m+8﹣2m﹣8
=﹣m2﹣4m,
=﹣(m+2)2+4,
∵﹣4<m<0,
当m=﹣2时,S有最大值为:S=﹣4+8=4.
答:m=﹣2时S有最大值S=4.
(3)设P(x,
 x2+x﹣4).
x2+x﹣4).
当OB为边时,根据平行四边形的性质知PQ∥OB,且PQ=OB,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为y=﹣x,
则Q(x,﹣x).
由PQ=OB,得|﹣x﹣(
 x2+x﹣4)|=4,
x2+x﹣4)|=4,
解得x=0,﹣4,﹣2±2
 .
.
x=0不合题意,舍去.
如图,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=﹣x得出Q为(4,﹣4).
由此可得Q(﹣4,4)或(﹣2+2
 ,2﹣2
,2﹣2
 )或(﹣2﹣2
)或(﹣2﹣2
 ,2+2
,2+2
 )或(4,﹣4).
)或(4,﹣4).


【点评】本题考查了三点式求抛物线的方法,以及抛物线的性质和最值的求解方法.


科目:初中数学 来源: 题型:
商场某种商品平均每天可销售40件,每件盈利60元.为减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多销售2件.
(1)每件商品降价多少元时,商场日盈利可达到3150元?
(2)商场日盈利能否达到3300元?
(3)每件商品降价多少元时,商场日盈利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线AB∥CD,直线EF与AB,CD分别交于点E,F,EC⊥EF,垂足为E,若∠1=60°,则∠2的度数为( )


A.15° B.30° C.45° D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
目前节能灯在城市已基本普及,今年云南省面向县级及农村地区推广,为相应号召,某商场计划用3800元购进节能灯120只,这两种节能灯的进价、售价如下表:
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
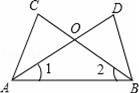
如图,△ABC与△ABD中,AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
你添加的条件是: .
证明: .

查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件:①367人中一定有两个人的生日相同;②抛掷两枚质地均匀的骰子,向上一面的点数之和大于2;③“彩票中奖的概率是1%”表示买1000张彩票必有10张会中奖;④如果a、b为实数,那么a+b=b+a.其中是必然事件的有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com