
商场某种商品平均每天可销售40件,每件盈利60元.为减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多销售2件.
(1)每件商品降价多少元时,商场日盈利可达到3150元?
(2)商场日盈利能否达到3300元?
(3)每件商品降价多少元时,商场日盈利最多?
【考点】一元二次方程的应用;二次函数的应用.
【分析】(1)根据日盈利=每件商品盈利的钱数×(原来每天销售的商品件数40+2×降价的钱数),把相关数值代入求解即可;
(2)根据日盈利=每件商品盈利的钱数×(原来每天销售的商品件数40+2×降价的钱数),整理后判断方程的根的情况即可;
(3)根据(1)得到的关系式判断出二次函数的对称轴,此时二次函数取到最值.
【解答】解:(1)设降价x元,由题意得:(60﹣x)(40+2x)=3150,
化简得:x2﹣40x+375=0,
解得:x1=15,x2=25,
∵该商场为了尽快减少库存,则x=15不合题意,舍去.∴x=25
答:每件商品降价25元,商场日盈利可达3150元;
(2)设降价x元,由题意得:(60﹣x)(40+2x)=3300,
化简得:x2﹣40x+450=0,
b2﹣4ac=1600﹣4×450=﹣200<0,
故此方程无实数根,
故商场日盈利不能达到3300元;
(3)设利润为y元,根据题意可得:
y=(60﹣x)(40+2x)=﹣2x2+80x+2400,
当x=﹣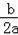
 =20时,y最大.
=20时,y最大.
答:每件商品降价20元时,商场日盈利的最多.


科目:初中数学 来源: 题型:
.8个一样大小的长方形恰好拼成一个大的长方形(如下图),若大长方形的宽为 8cm,则每一个小长方形的面积为 ( )
A.8cm2 B.15cm2 C.16cm2 D.20cm2

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.


查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com