
| A. | 正方形 | B. | 矩形 | ||
| C. | 菱形 | D. | 邻边相等的四边形 |
科目:初中数学 来源: 题型:选择题
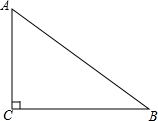 如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,若以点C为圆心,2.3为半径作⊙C,则直线AB与⊙C的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律大致如图所示(图中OABC为一折线),则这个容器的形状是( )
匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律大致如图所示(图中OABC为一折线),则这个容器的形状是( )| A. |  | B. |  | C. |  | D. | 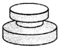 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
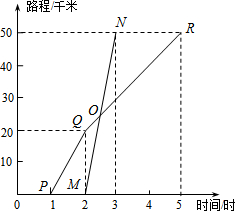 已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:
已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
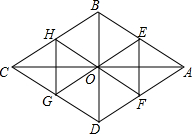 如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.
如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com