
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共5只.某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (结果精确到0.1);
(2)试估算口袋中黑球有 只,白球有 只;
(3)在(2)的结论下,请你用列表或树状图求出随机摸出两个球都是白球的概率.
【答案】(1)0.6;(2)2,3;(3)表格见解析,随机摸出两个球都是白球的概率为![]() .
.
【解析】
(1)根据统计表中第三行的数据即可得;
(2)用频率估计概率可得摸到白球的概率,再利用概率公式即可求得;
(3)先利用列表列出随机摸出两个球的所有可能的结果,再找出摸出两个球都是白球的结果,最后利用概率公式计算即可得.
(1)统计表中第三行的数据分别为:![]()
因此,当n很大时,摸到白球的频率将会接近0.6
故答案为:0.6;
(2)由(1)可得摸到白球的概率为0.6,设口袋中白球个数为x个
则![]() ,解得
,解得![]() ,即口袋中白球个数为3个
,即口袋中白球个数为3个
黑球的个数为![]() (个)
(个)
故答案为:2,3;
(3)由题意,将这5个球依次标记为![]() ,其中W表示白球,B表示黑球.因此,两次摸球的所有可能的结果有25种,如下表所示:
,其中W表示白球,B表示黑球.因此,两次摸球的所有可能的结果有25种,如下表所示:
第一次 第二次 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
它们每一种结果出现的可能性相等
从表中看出,两次摸出的球都是白球的结果有9种,即![]()
故所求的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
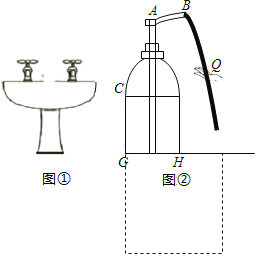
【题目】同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且a=﹣![]() .洗手液瓶子的截面图下部分是矩形CGHD.小王同学测得:洗手液瓶子的底面直径GH=12cm,喷嘴位置点B距台面的距离为16cm,且B、D、H三点共线.小王在距离台面15.5cm处接洗手液时,手心Q到直线DH的水平距离为3cm,若学校组织学生去南京进行研学实践活动,若小王不去接,则洗手液落在台面的位置距DH的水平距离是( )cm.
.洗手液瓶子的截面图下部分是矩形CGHD.小王同学测得:洗手液瓶子的底面直径GH=12cm,喷嘴位置点B距台面的距离为16cm,且B、D、H三点共线.小王在距离台面15.5cm处接洗手液时,手心Q到直线DH的水平距离为3cm,若学校组织学生去南京进行研学实践活动,若小王不去接,则洗手液落在台面的位置距DH的水平距离是( )cm.
A.12![]() B.12
B.12![]() C.6
C.6![]() D.6
D.6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
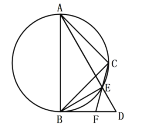
【题目】将一副三角板![]() 与
与![]() (其中
(其中![]() ,
,![]() ,
,![]() )如图摆放,
)如图摆放,![]() 中
中![]() 所对的直角边与
所对的直角边与![]() 的斜边恰好重合。以
的斜边恰好重合。以![]() 为直径的圆经过点C,且与
为直径的圆经过点C,且与![]() 相交于点E,连接
相交于点E,连接![]() ,连接
,连接![]() 并延长交
并延长交![]() 于F.
于F.
(1)求证:![]() 平分
平分![]() ;
;
(2)求![]() 与
与![]() 的面积的比值.
的面积的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”.
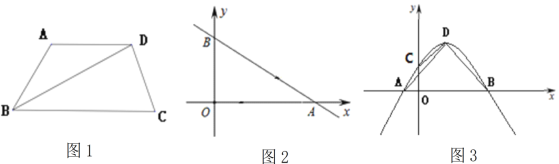
(1)如图1,BD平分∠ABC,AD∥BC,求证:四边形ABCD为“和睦四边形”;
(2)如图2,直线![]() 与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
(3)如图3,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与y轴交于点
轴交于A、B两点(点A在点B的左侧),与y轴交于点![]() ,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①
,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①![]() ;②顶点D在以AB为直径的圆上. 点
;②顶点D在以AB为直径的圆上. 点![]() 是抛物线
是抛物线![]() 上任意一点,且
上任意一点,且![]() .若
.若![]() 恒成立,求m的最小值.
恒成立,求m的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4
(1)随机摸取一个小球,直接写出“摸出的小球标号是3”的概率
(2)随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:
① 两次取出的小球一个标号是1,另一个标号是2的概率
② 第一次取出标号是1的小球且第二次取出标号是2的小球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
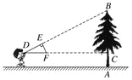
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50 cm,EF=25 cm,测得边DF离地面的高度AC=1.6 m,CD=10 m,则树高AB等于( )
A. 4 m
B. 5 m
C. 6.6 m
D. 7.7 m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 问题与探索
问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现:
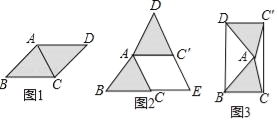
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是 .
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东55方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
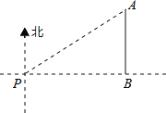
A.2cos55o海里B.![]() 海里C.2sin55海里D.
海里C.2sin55海里D.![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城市化建设的发展,交通拥堵成为上班高峰时难以避免的现象.为了解龙泉驿某条道路交通拥堵情况,龙泉某中学同学经实地统计分析研究表明:当![]() 时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
(1)当![]() 时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
(2)为使该道路上车流速度大于40千米/小时且小于60千米/小时,应控制该道路上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过该道路上某观测点的车辆数,即:车流量=车流速度×车流密度.当![]() 时,求该道路上车流量y的最大值.此时车流速度为多少?
时,求该道路上车流量y的最大值.此时车流速度为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com